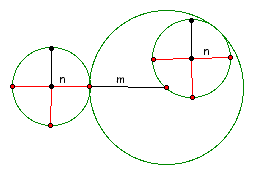
Now, it is time to find and prove an algorithm for determining the number of revolutions that a circle traveling around the outside or the inside of the circle will make. Recall out picture.

Here, the radius of the original circle has been labeled m and the radius of the inner and outer circles are n. So, now we claim that the the number of revolutions traveled around the original circle by the inner circle m/n -1 and that the number of revolutions traveled by the outer circle is m/n + 1.
The key for us was to realize that the number of revolutions hinges on the centers of the inner and outer circles. Although the animations show the circles traveling around the original circles, the centers of the circles are actually traveling around different circles that can be seen as the dashed circles in the next picture.
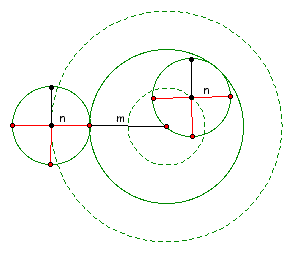
Now, we need to look at the ratio of the circumferences of the dashed circles to the original circle and this will determine the number of revolutions that the circles will make around the original circle.
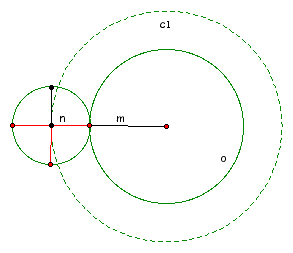
For this case, we will use the above diagram with original circle, o and the outer circle c1. The original circle has radius m and the outer circle has a radius of n. It is known that the ratio of the radii of two circles is equal to the ratio of their circumferences. So, c1 will give us the number of revolutions made by the outer circle to the ratio of the radius of the original circle.
The radius of the of c1 is equal to m + n, the sum of the radius of the original circle and the outer circle. Now, computing the ratio of c1 to o gives us: (m + n)/n. This could also be written as m/n + 1. This gives us our algorithm for working with the outer circle.
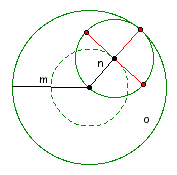
This case works just like the case above except the radius of the dotted circle is now m - n. So, when finding the ratio of the original circle to the dotted circle, it is (m - n)/n. Or, m/n - 1.