Assignment 12


 
 

Fibonnaci and Lucas Sequences

by

Behnaz Rouhani


 

In this assignment we generate a Fibonnaci sequence

f(n) = f(n-1) + f(n-2)

using f(0) = 1, and f(1) = 1.

First, we will construct the ratio of adjacent terms in the Fibonnaci sequence. Then, observe what happens as n increases. Further, we will explore the ratio of every second, third, fourth, fifth,...  terms.

Second, we will explore sequences where f(0) and f(1) are some arbitrary integers other than 1. In addition, we will learn about the Lucas Sequence.

A Fibonnaci Sequence is a sequence of numbers where f(n) = f(n-1) + f(n-2), and f(0) = 1, and f(1) = 1. We could explore this sequence using a spreadsheet. Below is a sequence where the first column represents n and the second column is the sequence produced.
 
 
 

n
f(n-1) + f(n-2)
0
1
1
1
2
2
3
3
4
5
5
8
6
13
7
21
8
34
9
55
10
89
11
144
12
233
13
377
14
610
15
987
16
1597
17
2584
18
4181
19
6765
20
10946
21
17711
22
28657
23
46368
24
75025
25
121393
26
196418
27
317811
28
514229
29
832040
30
1346269

 

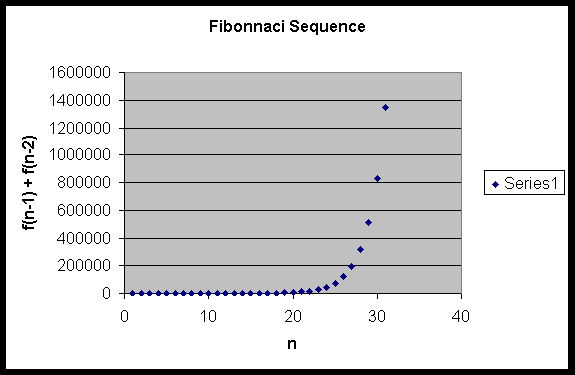
As we can see by the time n reaches thirty the number in the sequence is over one million. If we graph the above sequence we would have the following graph:
 
 




The graph appears to be exponential, so there must be a formula for evaluating the value of f(n) without depending on f(n-1) and f(n-2). In fact a formula does exist and it involves the golden ratio. The formula is:
 
 

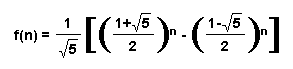
Now, we will address the following questions:
1. What is the ratio of each pair of adjacent terms in the Fibonnaci sequence, and what happens as n increases?
2. What about the ratio of every second, third, fourth, and fifth terms. Is there a pattern?
3. Special investigation.
4. What happens if we change f(0) and f(1) to some arbitrary integers?
5. What is a Lucas Sequence?

What is the ratio of each pair of adjacent terms in the Fibonnaci sequence, and what happens as n increases?  What about the ratio of every second, third, fourth, and fifth terms. Is there a pattern?

To investigate these questions we will use the spreadsheet. Click here to see the Excel spreadsheet where the first column is n, the second column is the Fibonnaci sequence, the third, fourth, fifth and sixth columns evaluate ratios as denoted below.

In this table,

f(n)/f(n-2)  = ratio of adjacent terms

f(n)/f(n-2) = ratio of every second terms

f(n)/f(n-3) = ratio of every third terms

and so on...
 

It is obvious that as n reaches a certain number, the ratio of adjacent terms reaches the limit of 1.618033989. This number is called the Golden Ratio. This ratio can also be written as

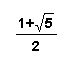
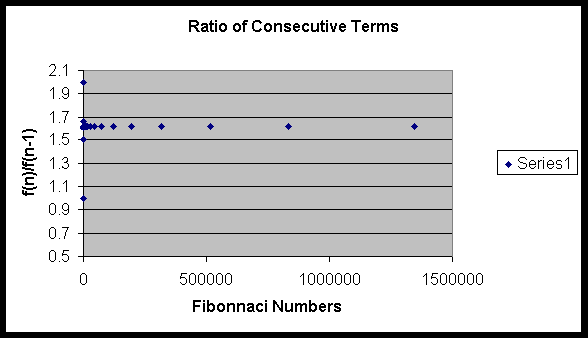
The following graph illustrates how the ratio of the adjacent terms, f(n)/f(n-1) converge to the golden ratio.
 
 




What can we say about the second, third, fourth and fifth ratios? It is interesting to note that:

Second ratio/first ratio = 1.618033989

Third ratio / second ratio = 1.618033989

Fourth ratio / third ratio = 1.618033989

Fifth ratio / fourth ratio = 1.618033989

The reason that the ratio of the ratios turns out to be the golden ratio is because

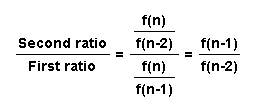
The above ratio of ratios reduces to the ratio of the terms f (n-1) and f (n-2), which is the golden ratio. This will hold true for all other ratios also.

Special Investigation

Now, what happens if we find the ratios in reverse order? That is, find the ratio of f (n-1)/f (n), f (n-2)/f (n), and so on. Click here to see the Excel spreadsheet for the ratios. In this case the ratio of the adjacent terms reaches the limit of 0.618033989, which is the inverse of the golden ratio. The inverse of the golden ratio could also be written as

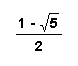
If you recall this is another part of the formula for the Fibonnaci sequence.

What can we say about the second, third, fourth, and fifth ratios? Do they reach a limit too? In this case:

First ratio / second ratio = 1.61803399

Second ratio / third ratio = 1.61803399

Third ratio / fourth ratio = 1.61803399

Fourth ratio / fifth ratio = 1.61803399

Can you tell why these ratios turn out to be the golden ratio?

What is a Lucas Sequence?

If we let f (0) = 1, and f (1) = 3, we will get the Lucas sequence. To see the sequence, click here.

As we can see the ratios reach the same limit, which is the golden ratio.

What happens if we change f (0) and f (1) to some arbitrary integers?

Let us explore the Fibonnaci sequence when:

To view the Excel spreadsheet that has the Fibonnaci sequence and the ratios for each of the above cases, click on the link. It is interesting to note that the ratios still reach the limit, the golden ratio. In fact all sequences similar to this regardless of the first two starting terms will have ratios that are equal to golden ratio.

Return to Behnaz Rouhani's Page