Assignment 6: Problem Solving
Using GSP
by
Melissa Silverman
Given any angle
ACB, construct a line XY such that AX=XY=YB.
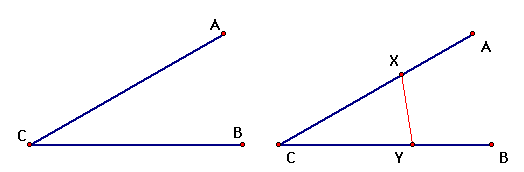
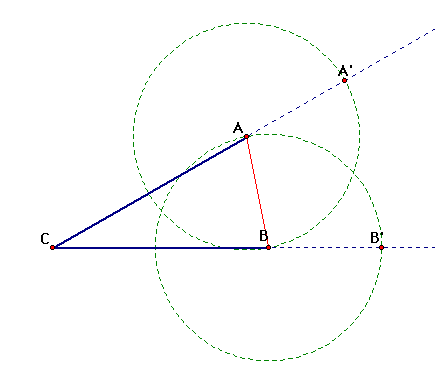
The first strategy to solve the
problem that I tried was circles, because all radii of a circle
are equal. I have to find equal lengths, so I thought I could
use circle radii to solve it. In the picture below, given angle
ACB, I can use circles to solve for A' and B' so that A'A=AB=BB'.
But that is not what the problem is asking. So strategy #1 failed.
I then decided to modify the circle
technique to stay more in line with the problem. I revised the
positioning of my circles to try and create a winning construction.
To my dismay, this failed as well.
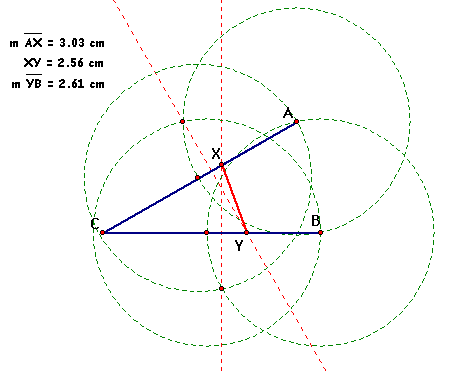 I began by making a circle with center
A and AB as its radius. Then I made a circle with center B and
BA as its radius. I then marked where those two circles intersect
the original angle. I made additional circles from there and found
myself in a big mess of circles. I made perpendicular lines from
a point where circles intersect to the original angle, which looked
like they would be close to points X and Y. So I constructed X
and Y. When I measured the segments, they were close in length
but not equal. So strategy #2 failed.
I began by making a circle with center
A and AB as its radius. Then I made a circle with center B and
BA as its radius. I then marked where those two circles intersect
the original angle. I made additional circles from there and found
myself in a big mess of circles. I made perpendicular lines from
a point where circles intersect to the original angle, which looked
like they would be close to points X and Y. So I constructed X
and Y. When I measured the segments, they were close in length
but not equal. So strategy #2 failed.
Circles, I decided, was not going to
be the way to an answer. I started thinking about other shapes
that might work. What about triangles? So I began tinkering with
triangles. If angle ACB is 60 degrees, then, using equilateral
triangles, you can find XY (indicated by the red line) so that
the three segments are equal.
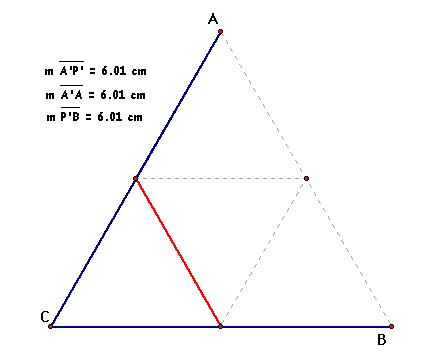 But again, this only works for one
angle, and the problem implies that it needs to work for any angle.
So strategy #3 has failed.
But again, this only works for one
angle, and the problem implies that it needs to work for any angle.
So strategy #3 has failed.
So I am afraid that my many attempts
to this problem failed. But that is a learning process in itself.
GSP is difficult in that something that seems very easy to solve
becomes more complex than you realize. As a student that has worked
a lot with GSP, I often find that I can't construct the answers
to what seem like simple problems because the way to solve it
seems too off the beaten path. I know the solution to this problem
has something to do with similar figures, for that was the clue
given in class. On my own brain power, the strategy of using similar
figures would never have occured to me. And even after trying
to use the clue, I could not create a winning construction.
Thinking about future middle school
students, I think this process might be really frustrating for
them (as it is frustrating for me too!). A problem that appears
easy seems to always have a really complicated construction to
go with it. It seems as though problems always have their own
"tricks" which are too hard to figure out on your own.
If I use GSP problem solving in the classroom, I need to make
sure that I choose problems that I know the students will be able
to answer without excessive stress and frustration, so that the
experience remains positive.
I could have thrown all of these ideas
out and tried to solve another problem, but I thought that maybe
showing everything that I thought of on my own to complete this
problem would make for an interesting write-up. On GSP I often
find myself going through this process, the process of trial and
error. To get the desired product, it sometimes takes a string
of ideas to get there. And sometimes even with multiple attempts,
the solution is something that I just would never have seen. I
think it is ok for students to know this, that sometimes problems
take a few tries. But the thoughts along the way are just as valuable
as the answer, because you never know what you might learn from
taking a detour.
Assignment 5
| Home Page | Assignment
7




