Assignment 8: Altitudes and Orthocenters
by
Melissa Silverman
Begin this investigation
by constructing any Triangle ABC. Construct the orthocenter of
Triangle ABC. If you construct the orthocenters of triangles HAC,
HAB, and HBC, their orthocenters fall on the vertices of the triangle.
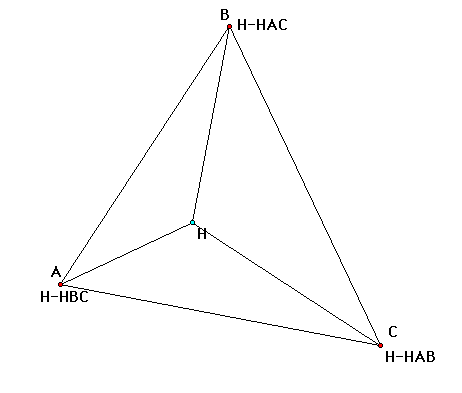
In the picture below, H is the orthocenter of Triangle ABC. Note
how the orthocenters of triangles HAC, HBC, and HAB are the same
as the vertices.
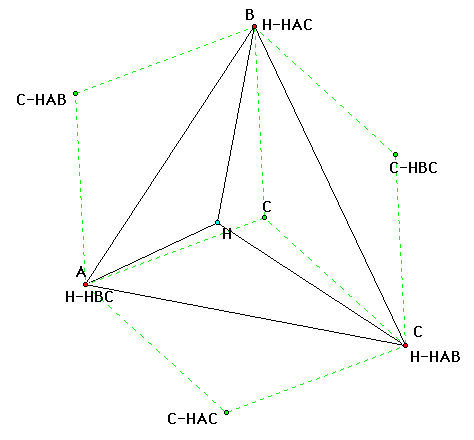
What can we say about the circumcenters
of triangles ABC, HAB, HAC, and HBC? The circumcenter of Triangle
ABC is inside the triangle. The circumcenters of the other three
triangles all fall outside of Triangle ABC. Connecting the four
circumcenters and the three vertices create a shape that looks
like a cube.
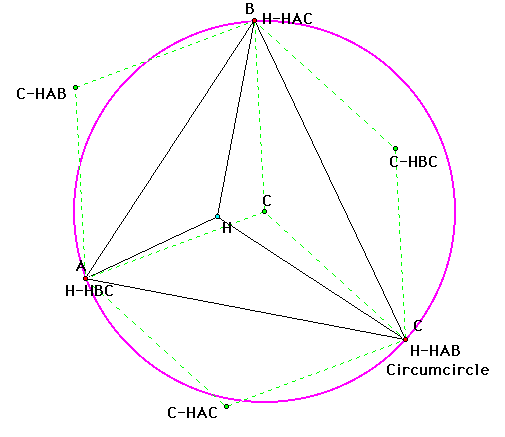
How to the circumcenters relate to
the circumcircle of Triangle ABC? Do they fall on the circumcircle?
Constructing the circumcircle of Triangle ABC reveals that two
of the circumcenters are outside the circumcircle, but one is
inside the circumcircle. The circumcenters do not fall on the
circumcircle and do not seem to be related to the circumcircle.
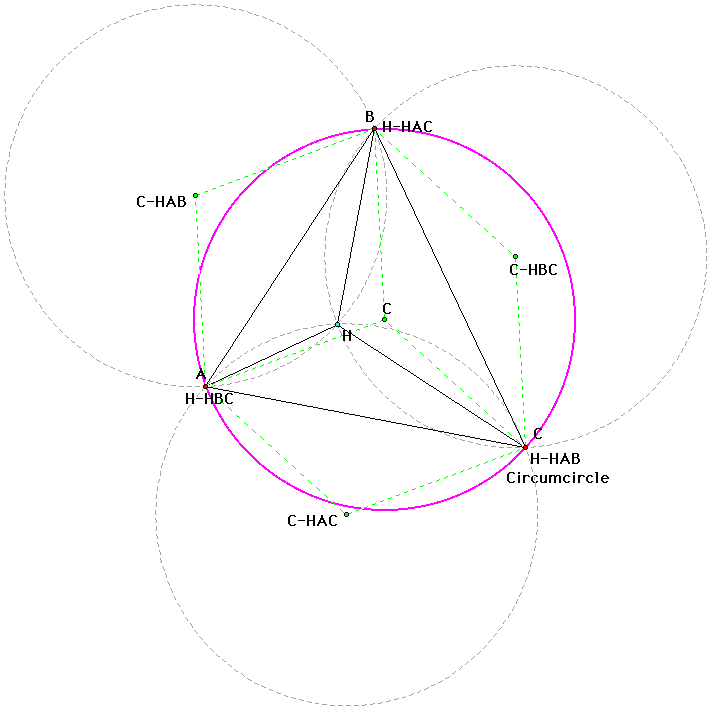
What about the circumcircles of triangles
HAC, HBC, and HAC? Constructing the circumcircles of these three
triangles shows that circumcircles go through the orthocenter
and two of the vertices of Triangle ABC. Reflecting the circumcircle
of Triangle ABC across the sides of Triangle ABC will result in
the circumcircles of triangle HAC, HBC, and HAB.
Assignment 7 | Home
Page | Assignment 9




