

Final Assignment
Ratios of Triangles
By: Denise Natasha Brewley
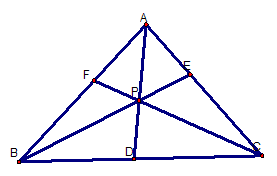
Consider any triangle ABC. I selected a point P inside the triangle and drew lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. The point where points D, E, and F intersect is the point of concurrency, namely point P. In this investigation, I will explore triangle ABC for various triangles and various locations of point P. I will then conclude with a proof of selected results.
PART A
Investigation #1 -- Varied Triangles
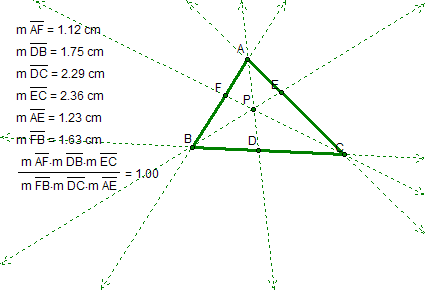
I began this investigation by considering the triangle above. I then explored the product of the following segments for various triangles. I looked at the typical cases, when triangle ABC is acute, obtuse, and right. Notice that in all cases, ratio of the line segments (AF)(BD)(EC)/(FB)(DC)(EA) = 1. Notice that the three line segments that make up triangle ABC is composed of two line segments itself. Essentially what this means is if we take "left hand side" segments of each segment of the triangle with the "right hand side" segments this ratio is equal to 1. I will come back to this result a bit later.
|
|
|
|
Investigation #2 - Varied Locations of point P
I started this part of the investigation by varying the position of point P. I located P at positions very close to the vertices of triangle ABC. The same result from Investigation #1 was true. But, some interesting things started to happen as I explored P further.
|
|
 |
|
It was pretty obvious what would happen if P was located on one of the vertices of triangle ABC. The intersection points through P vanished and I was just left with a arbitrary triangle. I did the this exploration for various shapes of triangle ABC, but I only present the result for one vertex for each shape explored.
|
|
|
|
I then took P outside of triangle ABC. Note, I wanted to see what would happen to the values of the line segments, indicated at the left of each triangle, if P was located outside one of the sides of triangle ABC. Some interesting things occurred. Depending on the side the P was outside of, the other two line segments that intersect at point P disappeared. In the first case, since P is outside of side AB, the measure of these sides were given along with the distance that P was from point A.
When P is outside of side AC, the same thing happens. The difference however is, line segment BE appears to be extended with a point P on that line. Finally, if we look at when P is outside of BC, that same thing happens again. I asked myself why would point P be an extension of each respective segment? What I concluded was, that if point P is outside of the triangle ABC, then there would not be a common intersection point to start with that was inside the triangle. And so, P would just be an arbitrary point in the plane that would be on a line segment constructed from the opposite vertex from P's location.
|
|
|
|
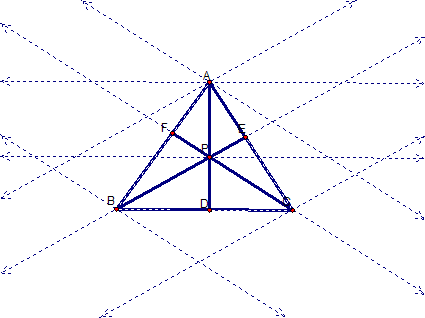
I wanted to know if we would get the same results if triangle ABC was constructed using lines rather that line segments. So I considered the triangle below. Please Click here to explore in GSP for various locations of point P of the triangle.
So now I know that I am limited in discussing point P, when triangle ABC is constructed using line segments. When triangle ABC is constructed using lines, our results are more interesting. I gave a few examples below when point P is outside the triangle. Notice that all of the ratios are still in tact.
|
|
|
PART B - The Proof
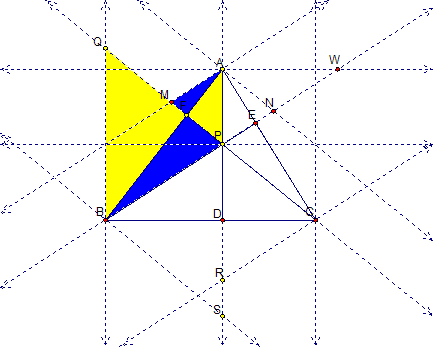
In the second part of this investigation, I attempt to prove that the result from Part A holds. So I begin by constructing parallel lines to line all of concurrent segments of triangle ABC. I also extend the sides of ABC as well. Our goal in doing this is to find similar triangles so that we can generalize about triangle ABC.
After the lines were extended. I went about finding similar triangles. In this case, triangles BQF and AFP are similar in addition to triangles AMF and BFP. Some results now follow:
BF/AF = QM/PF = BQ/AP,
BD/CD = BP/CR = BS/PC,
and
CE/AE = CP/AN = CW/AP.
Continuing in the same manner, we continue to construct more similar triangles. In this case we can say that
QB/PD = BC/DB
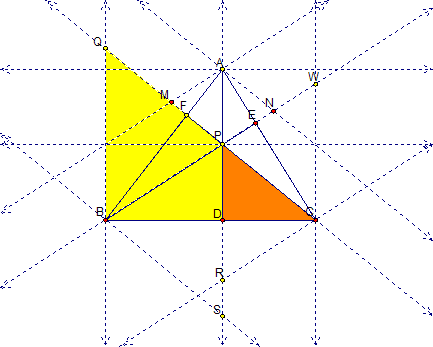
And in this case we can say that
CQ/PQ = DP/CW
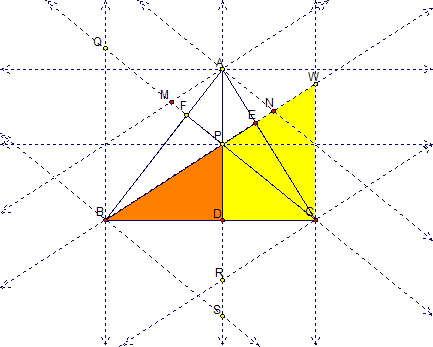
If we take the two previous equations namely QB/PD = BC/DB and CQ/PQ = DP/CW, we can solve both equations for DP. So we obtain the following,
DP = (CD)(BM)/CB
and
DP = (BD)(CK)/CB
Each equation has a CB in the denominator and this cancels. Simplifying further, we get two new ratios
BM/CK = BD/CD
If we look at triangle ABC, we can also see that
FB/AF = NA/BS
and
CR/AM = CE/AE
Now, if we consider the original equation that we are trying to prove, (AF)(BD)(EC)/(FB)(DC)(EA) = 1, this can be rearranged. And so it follows that we get,
(EC)(AF)(BD)/(EA)(FB)(DC) = 1
And so we have,
(EC/EA)(AF/FB)(BD/DC) = 1
From our previous equations, this simplifies to
(CW/AP)(AP/PQ)(PQ/CW) = 1
QED.
PART C
To conclude this investigation, let's again consider when the point P is inside of triangle ABC. The ratios of the areas of triangle ABC and triangle DEF will always greater than or equal to 4.
|
|
|
|
|
|
I wanted to know when would the ratio of triangle ABC and triangle DEF always equal 4. So I constructed the midpoint of AB and AC. Each of these points respectively are point N and point O respectively. I then chose a random point on BC -- this was point W and constructed triangle NOW. Above I give two locations of point W.
CONCLUSION
So to answer the question, the ratio of triangle ABC and triangle DEF will always equal to 4 when any two midpoints on triangle ABC are identified. So it follows that this would work if the point P is the also the Centroid of triangle ABC -- Click Here to see it in GSP.