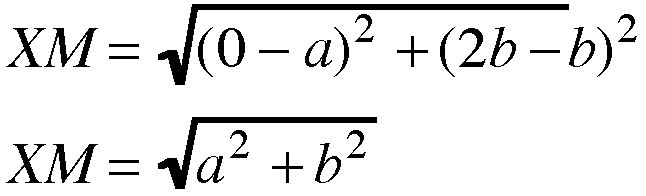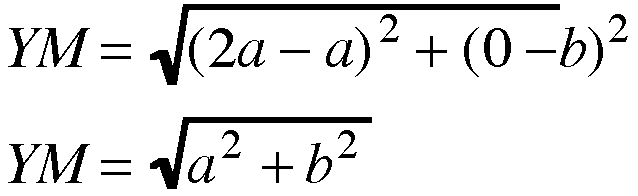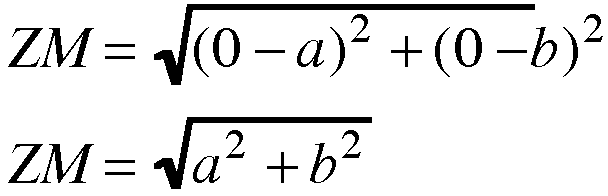The Coordinate Geometry Proof
Nicole Mosteller
EMAT 6690
This
proof involves the application
of the Midpoint Formula and the Distance Formula both in Relation
to Coordinate Geometry.
Given a right triangle XYZ with the
median of the hypotenuse labeled M.
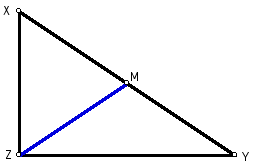Figure 1: Given.
Let's impose our right triangle onto
a coordinate graph.
For simplicity sake, let's
use Quadrant I and place our right angle at (0, 0) so that
the legs of our right triangle fall
along the x-axis and y-axis.
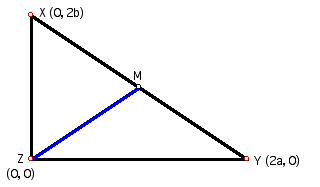Figure 2: The right triangle with variable coordinates.
**Why is the coordinate of X (0, 2b) and the coordinate
of Y (2a, 0)? Using the coefficient values of 2 on for these
coordinates allows for algebraic ease later in the proof. Because
a and b are not restricted to the integers, this notation does
not imply respective coordinates are even.
Since we know that point M is the midpoint
of the hypotenuse,
the coordinate of M if found using
the midpoint formula.
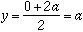
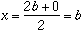
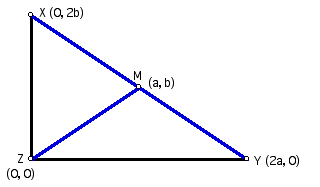
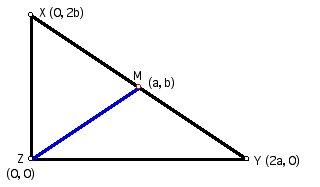Figure 3: The coordinate of M is (a, b).
Now that we have the coordinates of
each point,
let's use the distance formula to find
the distance between the endpoints of
segments XM, YM, and ZM.
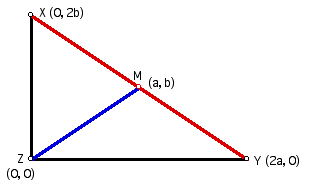Figure 4: Using the known coordinates, use the distance formula
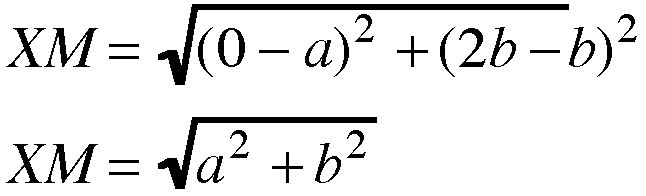
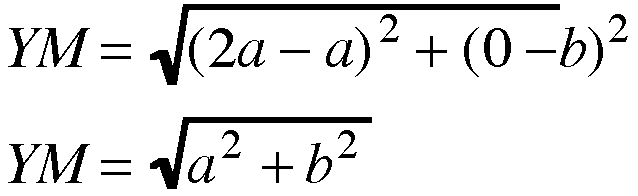
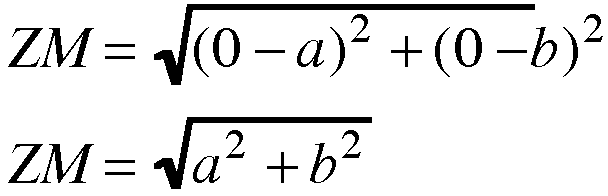
By substitution, we are able to arrive
at the conclusion
XM = YM = ZM.
By definition, point M is equidistant
from points Z, X, and Y.
So, the midpoint M is eqidistant from
all of the vertices of the right triangle.
Return
to Intro | Proof
#1 | Proof #2 |
Proof #3 | Proof #4 | To
Nicole's Page