Nicole Mosteller's Parallel Line Proof

The Parallel Proof
Nicole Mosteller
EMAT 6690

This proof requires the application of parallel line properties and isosceles triangle properties.

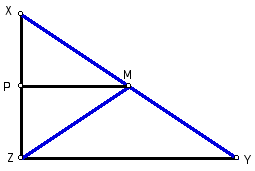
Given a right triangle XYZ with the median of the hypotenuse labeled M.

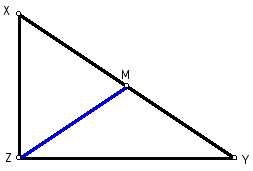Figure 1: Given

First, construct a line through point M that is parallel to segment ZY.

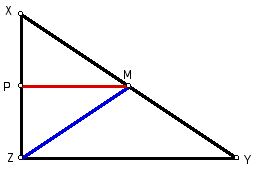Figure 2: PM is parallel to ZY.

By extending a common parallel property, we know that if a segment bisects

one side of a triangle (side XY) and is parallel to another side of the triangle (side ZY),

then it must also bisect the third side of the triangle (side XZ).

And so, XP is congruent to ZP.

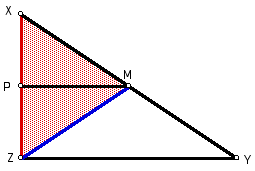Figure 3: MP bisects XZ.

Since segment MP is parallel to segment ZY (by construction) and segment ZY is perpendicular to segment XZ,

then segment MP must also be perpendicular to segment XZ.

By definition, MP is an altitude of triangle XMZ

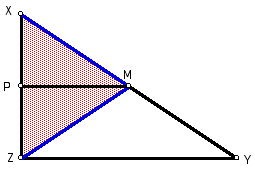Figure 4: Triangle XMP is isosceles.

Because MP is both a bisector and an altitude of triangle XMP, we know that triangle XMP is isosceles

with side XM congruent to side ZM.

Segment ZM is congruent to segment XM (legs of isosceles triangle), and

segment XM is congruent to segment YM (definition of median).

By transitive property, ZM = XM = YM.

Figure 5: ZM = XM = YM.

So, the midpoint M is eqidistant from all of the vertices of the right triangle.