The Rectangle Proof
Nicole Mosteller
EMAT 6690
This proof requires the application
of properties of parallelograms and rectangles.
Given a right triangle XYZ with the
median of the hypotenuse labeled M.
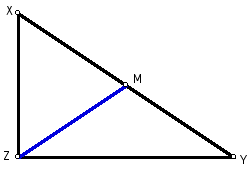Figure 1: Given.
To complete this proof it is necessary
to add a few lines.
Below, segment AY has been constructed
parallel to segement ZX, and
segment XA has been constructed paralled
to segment ZY.
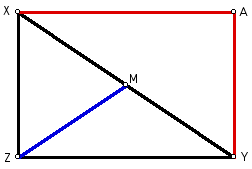Figure 2: The rectangle.
By definition, quadrilateral XAYZ is
a parallelogram with right angles (because angle XZY is right).
XAYZ is better known as a rectangle.
The remainder of our proof involves
the established properties of parallelograms and rectangles.
The figure below shows the rectangle
with diagonals XY and AZ drawn.
Because XAYZ is a parallelogram, the
diagonals bisect each other.
XM = YM and AM = ZM.
Because XAYZ is a rectangle, the diagonals
are congruent.
XM = YM = AM = ZM.
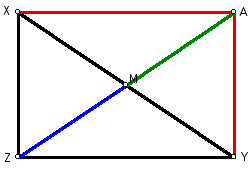Figure 3: XM = YM = AM = ZM.
By definition, point M is equidistant
from points Z, X, and Y.
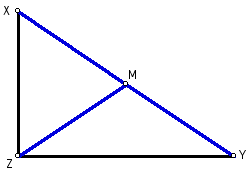Figure 4: XM = YM = ZM.
So, the midpoint M is eqidistant from
all of the vertices of the right triangle.
Return
to Intro | Proof
#1 | Proof #3
| Proof #4 | Proof
#5 | To Nicole's Page