Given segment AB with parallel intersecting segments AE and BC on the same side of AB. Construct the segments AC and BE, intersecting at F and construct the segment FG parallel to AE and BC with G on AB.
Prove:
Clearly, one approach is to use similar triangles.
Add the two equations together, substitute and symplify. . .
INTERPRET. Let FG = x, AE = a, and BC = b. Then
or 
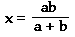
For positive a and b, x is ONE-HALF the harmonic mean of a and b.
Reference:
Charosh, M. (1965) Mathematical Challenges. Washington, DC: National Council of Teachers of Mathematics. Problem 30.
Given two line segments, find geometric constructions of a segment with length that is the harmonic mean of the lengths of the given two segments.