An Obtuse Triangle Relationship
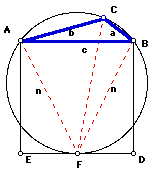
Suppose that triangle ABC has integral side lengths
a = BC, b = CA, c = AB and side AB is the
longest side. Construct a square ABDE on the side of AB remote
from C. Suppose furthermore that side DE of the square ABDE is
tangent to the circumcircle of triangle ABC.
- (1) Express c as a function of a and b.
-
- (2) Find (non-similar) triangles which satisfy the hypotheses
of the problem.
-
- (3) Is the set of non-similar triangles which satisfy the
hypotheses of the problem finite or infinite? Why?
-
Reference: This is problem SSM 4697, Proposed
by V. C. Bailey, Naples, Florida, in the January 1999 issue of
School Science and Mathematics.
- Click here for a GSP Sketch.
Move point C to different spots on the minor arc AB to view different
triangles with this configuration.
-
- Strategy: Finding an expression for c in terms
of a and b can ignore the requirement for integer
values. Once we have an expression for (1) we can use it to search
for integer values of a, b, and c.
-
- Must the point of tangency of the circumcircle to DE be at
the midpoint? Why?
-
- Draw in segments FA, FC, and FB.
- Let the lengths of the sides AF and BF be on length n.
Can you solve for n in terms of c?
-
- What next? Hint?
- More of a Hint.
- Solution to Part (1)
- PART (2)
-
- When we have c as function of a and b,
whether or not the values are integer, then Part (2) becomes
a search for integer values to satisfy the function. Since 5
and 6 are relatively prime the search for integer values of a
and b where the expression under the radical is a perfect
square can be limited to where at least one of them is a multiple
of 5. For example, a = 9, b = 10, yields c
= 17.
-
- Find others. Click here
to see a short list of others.
PART (3). How could this be proved?
Return to EMAT
4600/6600 page