

There are a total of 12 problems posed on this page.
Given a triangle ABC.
See Also: Triangle/Steinhaus
Construct triangle DEF as follows:
Extend a ray from A through B and locate D such that AB = BD
Extend a ray from B through C and locate E such that BC = CE
Extend a ray from C through A and locate F such that CA = AF
1. What can be said about these two triangles and any relationships between them?
Click HERE for a GSP file to explore this construction.
2. Show that the area of triangle DEF is 7.00 times the area of triangle ABC.Hint? This will open a GSP file . . .
3. Show that triangle ABC is not similar to triangle DEF.
4. Do triangle ABC and triangle DEF have the same centroid?
Construct points G, H, and I on DE, EF, and FD respectively by extending AC to intersect with DE, BA to intersect with EF, and CB to intersect FD.
5. Show that
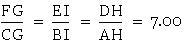
6. Show that G, H, and I are trisection points of the sides DE, EF, and FD respectively.
7. Construct the other trisection points on each side and label them J, K, L.
Construct FJ, DK, and EL. Make their intersections M, N, and O.
8. What can be said about triangles ABC and MNO?
9. What fraction of the area of Triangle ABC is the GREEN irregular hexagon formed by the overlap of triangles ABC and MNO?
Click HERE for a GSP file with this construction.
Extensions10. Explore this problem with ABC constructed as an EQUILATERAL triangle.
11. Explore with Triangle ABC a right triangle.
12. Develop the construction with the vertices of triangle DEF only one-half the extension of the sides of ABC