
The Pedal Triangle (continued)
By
Sharon K. O’Kelley
Why is the Simson Line Created when P is on the
Circumcircle of the Original Triangle?
Consider figure 5. Recall
that points A, B, and C are collinear and are also the vertices of the degenerate
pedal triangle with P as its pedal point. Here, we will explain why A, B, and C
are collinear and thus create the Simson Line.
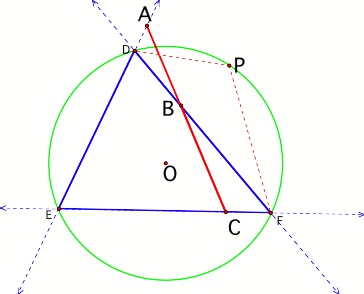
Figure 5
In figure 5, the original
triangle has been labeled as DFE. Notice that points D, P, F, and E can be joined
to create a cyclic quadrilateral meaning that the quadrilateral is inscribed on
the circle. In cyclic quadrilaterals, opposing angles are supplementary;
therefore…
![]()
![]()
Next, consider triangle
AEC which has its own circumcircle S as shown in purple in figure 6. Note that
P lies on circle S as well as circle O.
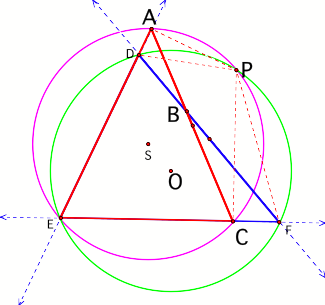
Figure 6
Circle S contains the
cyclic quadrilateral APCE. Since angle E and angle APC are opposing angles of
the cyclic quadrilateral, they are also supplementary; therefore…
![]()
It can be concluded then
through substitution that…
![]()
Using the angle addition
postulate, the following relationships can be established…
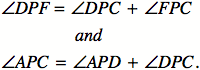
![]()
Since these two angles
share common angle DPC, angle DPC can be subtracted from both thus yielding…
![]()
Next, consider that there
are two other circumcircles involving point P as shown in figure 7.
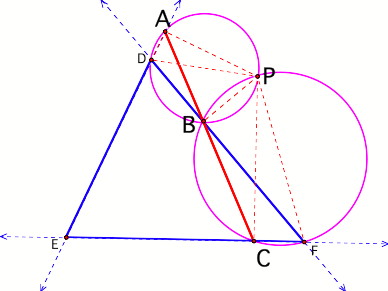
Figure 7
Because quadrilaterals
PFCB and PADB are cyclic quadrilaterals on their respective circles, the
following relationships can be established…
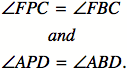
Using substitution
establishes that…
![]()
Because these two angles
are equal, they can be verified as vertical angles; therefore, points A, B, and
C are collinear making the pedal triangle degenerate and thus establishing the
Simson Line.
What connection does the
Simson Line have to Ptolemy’s Theorem? Go here for the answer.