A Special Case of the Pedal Triangle

By Sharon K. O’Kelley

Introduction

This presentation provides an overview of the degenerate case of the Pedal Triangle, explores the resulting Simson Line, and provides a connection between the Simson Line and Ptolemy’s Theorem. The goal here is to demonstrate for an advanced high school math student or teacher how various mathematics topics can be connected together – i.e., to show the relationships that can be established through exploration and explanation. Some of the topics addressed here are altitudes of triangles, circumcircles, cyclic quadrilaterals, and trigonometry. This presentation is centered around constructions and observations made from the use of Geometer’s Sketchpad.

The Pedal Triangle

Given a point P either inside or outside a triangle, a Pedal Triangle is constructed when the feet of the perpendicular segments joining P to the sides of the original triangle are joined. In figures 1 and 2, triangle ABC is the Pedal Triangle for pedal point P.

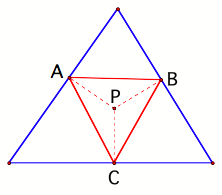
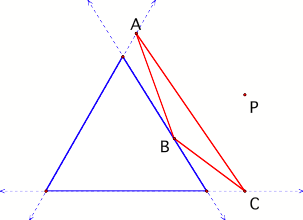
Figure 1 Figure 2

The Degenerate Case of the Pedal Triangle

Consider figure 3 in which circumcircle O has been constructed for the given triangle. Note that point P is off the circumcircle and the vertices of triangle ABC are noncollinear.

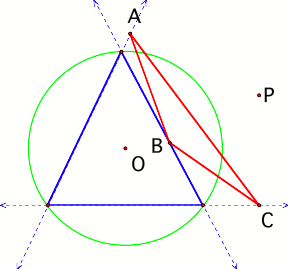
Figure 3

Using Geometer’s Sketchpad, point P can be merged with the circle. When this occurs, the Pedal Triangle collapses or becomes degenerate which means the vertices of A, B, and C become collinear thus creating the Simson Line. In figure 4, line AC containing point B is the Simson Line.

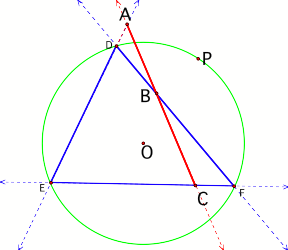
Figure 4

No matter where P falls on the circumcircle, the Pedal Triangle remains collapsed as the Simson Line.

To download an animation of the Simson Line using Geometer’s Sketchpad, click here.

For an explanation behind the creation of the Simson Line, go here.

Return