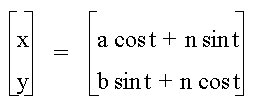Parametric Equations
November 13, 2010
This investigation makes use of Graphing Calculator. The file used can be downloaded here.
Please note: you might need a plugin to play the animations in
this page.
3. More Advanced Sine and Cosine
4. Animated
1. Quick introduction
Here is a quick introduction to parametric equations from Brightstorm (if it's not available, just wait a few seconds and click play again):
2. Basic Sine and Cosine
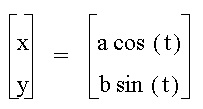
Figure 2.1: Parametric equations
Now we'll have a look at the effect of a and b on the equations:
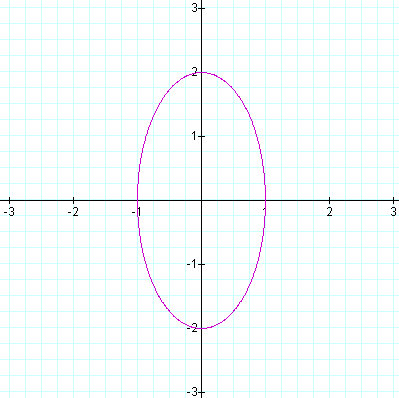
Figure 2.2: a = 1 and b = 2
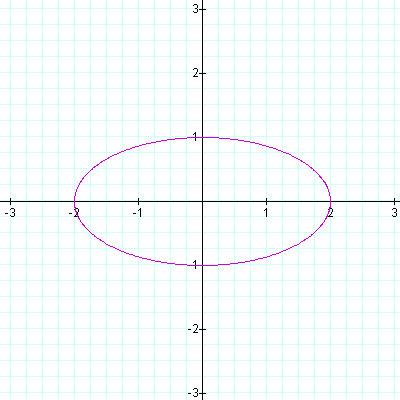
Figure 2.3: a = 2 and b = 1
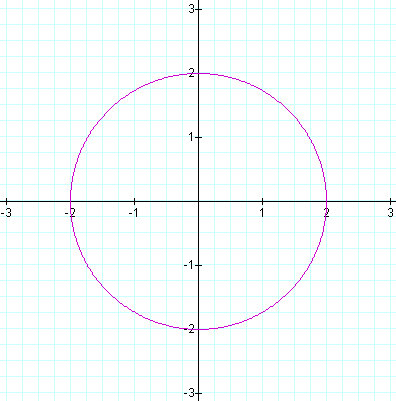
Figure 2.4: a = 2 and b = 2
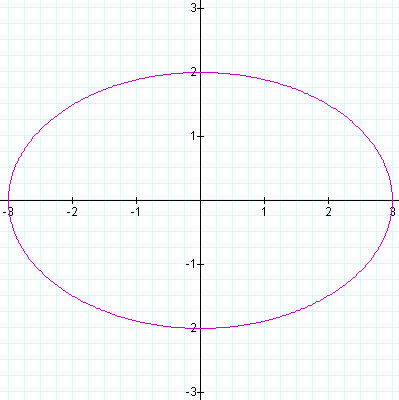
Figure 2.5: a = 3 and b = 2
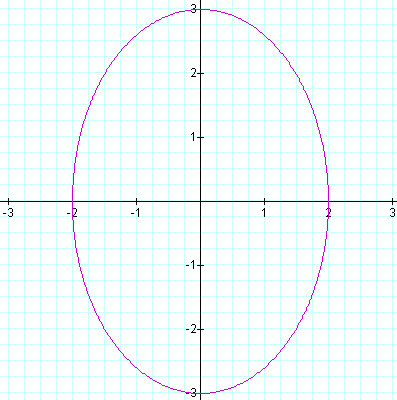
Figure 2.6: a = 2 and b = 3
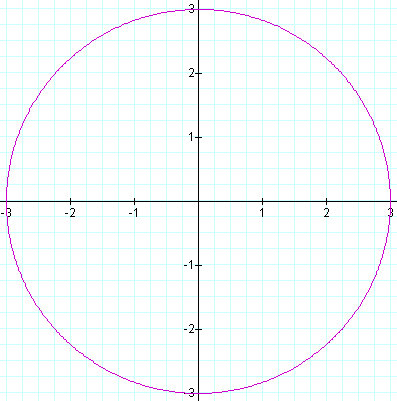
Figure 2.7: a = 3 and b = 3
In the next section we look at more advanced parametric equations.
3. Advanced Sine and Cosine
We expand on the previous set of equations:
- a = 1,
- b = 1 and
- differering values for n:
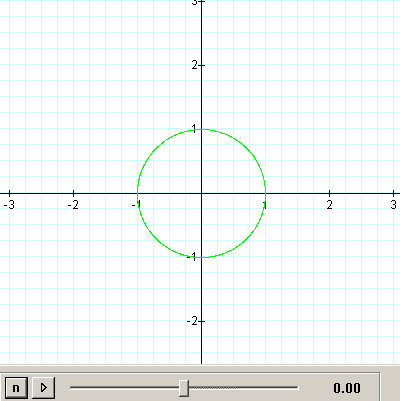
Figure 3.2: h = 0
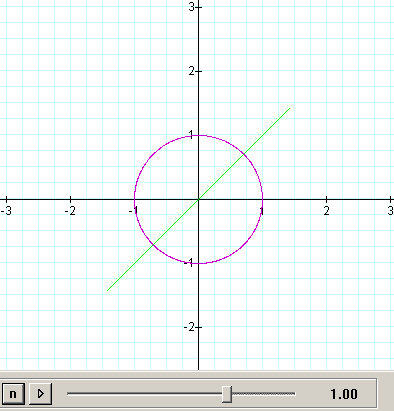
Figure 3.3: h = 1
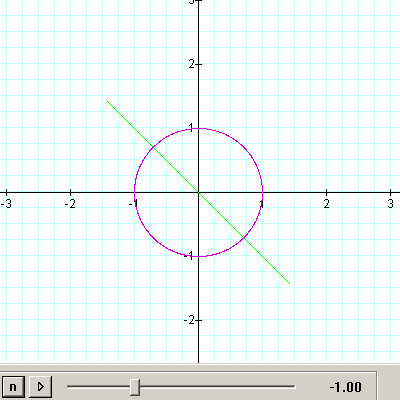
Figure 3.4: h = -1
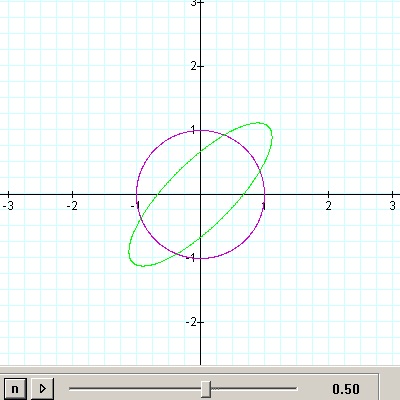
Figure 3.5: h = 0.5
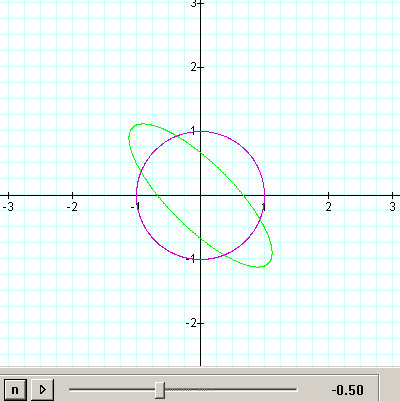
Figure 3.6: h = -0.5
4. Animated
This is how the graphs would look by moving the the value h from -2.5 to 2.5 in a 100 steps:
5. Interesting Application
- Locus of a triangle:
- Spirographing:
In closing, this is how one artist used spirographing to create some nice graphics: