Polar Equations

 December 9th, 2010

In this investigation we look at a polar equation: first there will be a quick introduction followed by some variations of the variables in the equation just to get a feel for what kind of effect they will have on the equation.

Please note: you might need a plugin to play the animations in this page.

1. Quick Introduction

2. Our equation 

3. Some variations on a,b and k

4. Windmill

 

1. Quick Introduction

Here is an introduction to polar coordinates and equations:

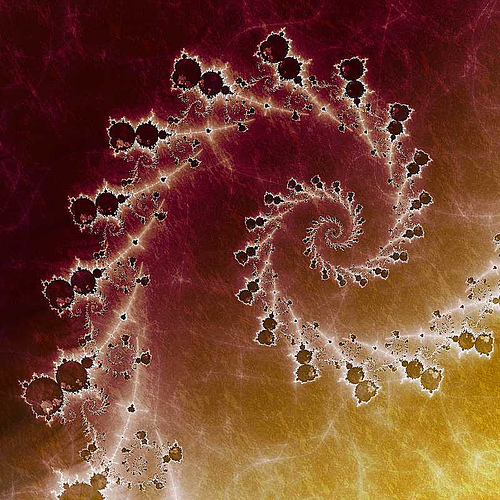
2. Our Equation

This is the polar equation we will be working with:
This is what the graph looks like:
To show how this is different from cartesian coordinates, consider the following changes we make to the variable theta. As it moves from 0 to pi (or about 3.14), we get half a rotation, and as we continue from pi to twice the value of pi (about 6.28) we have a full rotation.

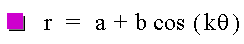
3. Variations on a, b and k

Note what happens when a = b:



Now see what happens if a < b:


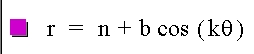
And if b < a:



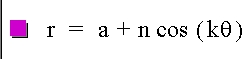
Finally, let's look at different values of k (notice what happens when k is an integer):


If k = 1 then we have one leaf of the rose, k = 2 has two leaves etc.

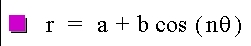
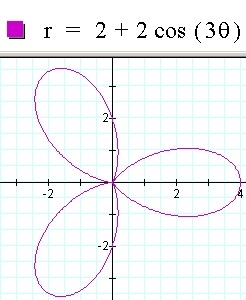
4. Windmill

Let's keep k constant at 3 so that we three leaves:

 This is what happens when we move a given this equation:

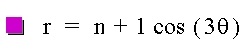
Now we do the same with b:


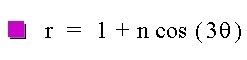
We can also add a value to theta which would have caused a left or right shift in Cartesian coordinates, now has this effect:


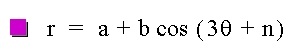
Now, by using what we know about the effects of the variables a,b and k, we can create a pretty nice animation (we will keep a = b and increase theta rapidly with some n):



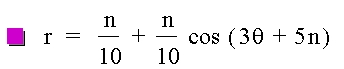
I hope you enjoyed a quick introduction to polar equations.