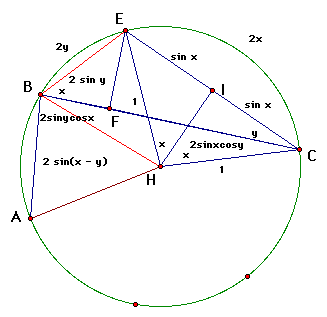
The Theorem of the Broken Chord also leads to the above trig identity. This is also based on the diagram that was worked with on the broken chord extentions page. As a refresher, see the diagram below.

First, find the length of segment BC. BC intersects arc BEC which is made of minor arcs BE and EC. These minor arcs have known lengths of 2y and 2x. So, arc BEC has length of 2x + 2y. Now, based on what we previously proven, the length of BC is 2 sin (x + y).
Second, BC is made of segments BF and FC which have lengths 2 sinxcosy and 2 sinycosx. This leads to the following equation.
Substitution of the lengths of the sements yields:
Divide by 2 and the result is
Finally, reorder the equation so that it is in the form of our known trig identity which is: