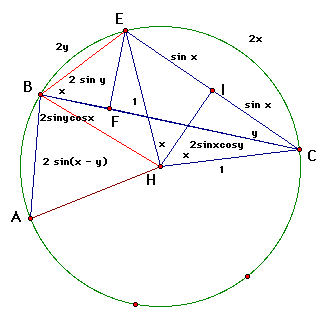
The theroem of the broken chord leads us to the trig identity above. So, we start by looking at the diagram that was created on the previous page. To refresh our memory, the diagram is below.

Recall the theorem of the broken chord states that AB + BF = FC. The lengths are listed above on the diagram and have been proven correct on the previous page. So, substitut the lengths of these segments into the formula and we get:
Now, divivide by 2 which yield:
Finally, solve for sin(x-y) and we get the desired identity.
Return to the Broken Chord Main Page