The Circle Proof
Nicole Mosteller
EMAT 6690
This proof requires application
of the definitions in relation to the parts of a circle and properties
of inscribed angles.
Given a right triangle XYZ with the
median of the hypotenuse labeled M.
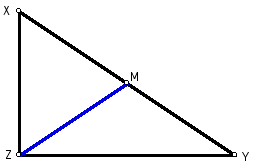Figure 1: Given.
The first step in our proof is to inscribe
the right angle XZY in a circle.
The circle has the center to be point
M and the radius segment ZM.
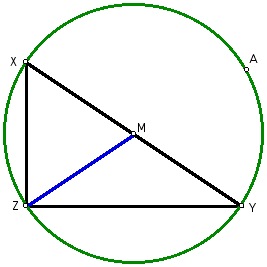Figure 2: ZM is a radius of Circle M.
Remember the angle that we inscribed
is a right angle. Inscribed right angles intercept
arcs that measure 180 degrees (semicircles),
and this makes the hypotenuse of any inscribed right
triangle the diameter of the circle.
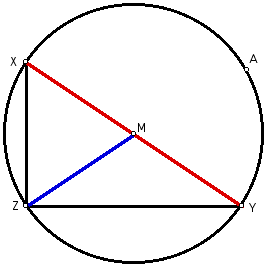Figure 3: XY is a diameter of Circle M.
Since XY is a diameter of Circle M,
and point M is the midpoint of XY,
by definition, XM and YM are radii
of Circle M.
Since segments ZM, XM, and YM are all
radii of the same circle, then
ZM = XM = YM.
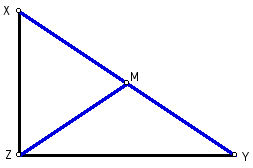Figure 4: ZM = XM = YM.
By definition, point M is equidistant
from points Z, X, and Y.
So, the midpoint M is eqidistant from
all of the vertices of the right triangle.
Return
to Intro | Proof
#2 | Proof #3
| Proof #4 | Proof
#5 | To Nicole's Page