Nicole Mosteller's Similar Triangle Proof


The Similarity Proof
Nicole Mosteller
EMAT 6690

This proof requires applications of reflection of a triangle over a line and similar triangles.

Given a right triangle XYZ with the median of the hypotenuse labeled M.

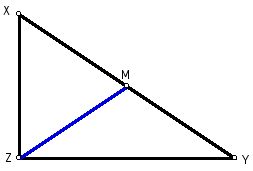Figure 1: Given.

Using property of reflection, reflect triangle XYZ across segment YZ.

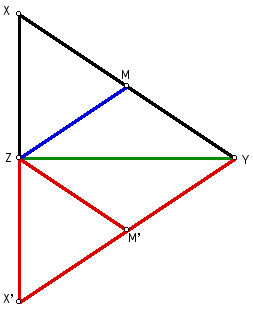Figure 2: Reflection of triangle XYZ.

The reflection of M is the point M'. When these points are connected, we have the

the additional segment MM' in our figure.

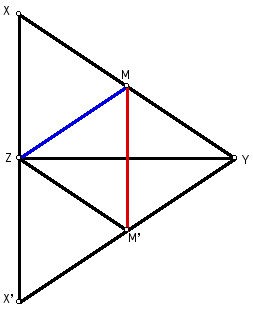Figure 3: Segment MM'.

Now, let's observe the various triangles created by the reflection.

Triangle MYM' is similar to triangle XYX' (by SAS).

Since M is the midpoint of segment XY,

these triangles are similar by a scale factor of 1:2

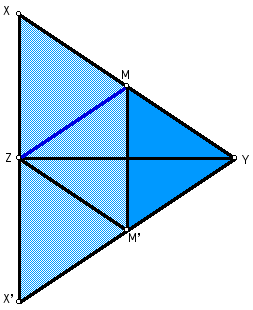Figure 4: MYM' is similar to XYX'.

Triangle XMZ is similar to triangle XYX' (by SAS as well).

The reflection of X to X' also makes these triangles similar by a

scale factor of 1:2.

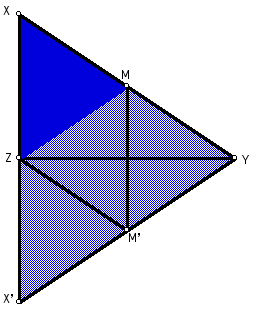Figure 5: XMZ is similar to XYX'.

Since triangle MYM' and triangle XMZ are similar to the same triangle and

because the similarities are with the same scale factor 1:2,

then triangle MYM' must be congruent to triangle XMZ.

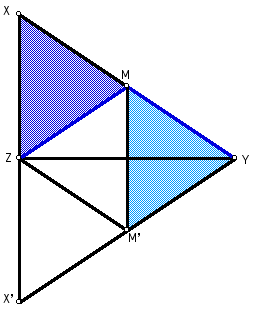Figure 6: MYM' is congruent to XMZ.

This triangle congruence leads to the following list of congruences:

ZM = M'Y (CPCTC), M'Y = MY (reflected), MY = MX (def. of median).

By the transitive property, ZM = MY = MX.

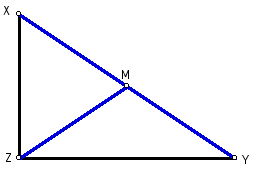Figure 7: ZM = MY = MX.

So, the midpoint M is eqidistant from all of the vertices of the right triangle.