Case 1:
Let us look at a few examples. First, let a = 1 and b = 1.
When k = 1, we have the following graph:
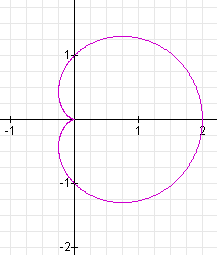
When k = 2, we have the following graph:
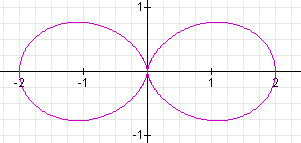
When k = 3, the graph is the following:
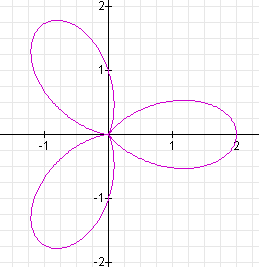
It appears that when | a | = | b |, k determines the number of "leaves" that the "rose" will have.
Let's look at a few more examples.
The graphs of
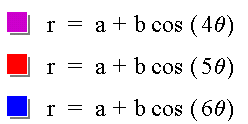
appear below.
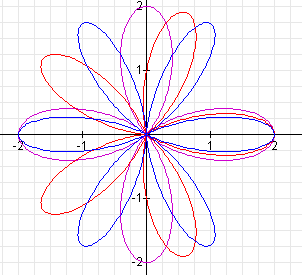
As before, k determines the number of leaves. When k = 4, the rose has four leaves. When k = 5, the rose has five leaves. When k = 6, the rose has six leaves.
In each case, the leaves are equally spaced around the
origin. The end of the first leaf (the point that is farthest from the
origin) is on the x-axis. Each leaf can be rotated 2
/k
radians to get to the next leaf.
In this case | a | + | b | = 2, and the length of each leaf (the distance from the origin to the end of each leaf) is 2 units. Is this always the case? Let's look at a few more examples.
Let's let a = b = 2. Then we have
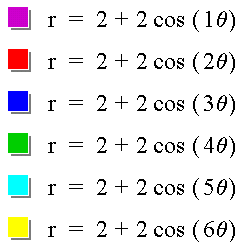
and the graphs look like
In this case, | a | + | b | = 4, and the length of each leaf is four units. The end of one of the leaves is the point (0, 4).
What happens when a and b are both negative?
Let's compare the graph of the following two equations:
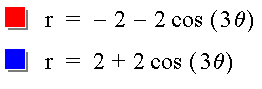
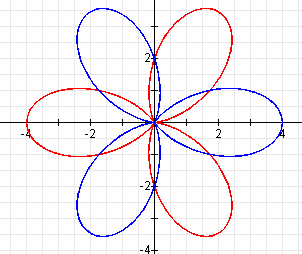
In this example, k is odd, and the graph when a
and b are both negative is the graph when they are both positive but
rotated /k
radians.
Now let's let k be even and look at the following graph:
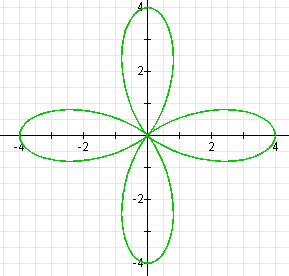
This graph is exactly the same as the above graph of
What happens when a and b have opposite signs?
Let's consider the case where a is negative and b is positive. Let's let k be odd, and look at a few graphs.
The equations
have the following graphs:
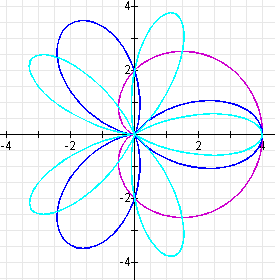
These graphs are exactly the same as the graphs when a and b are both positive.
Let's let k be even, and consider the following equations:
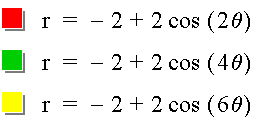
They have the following graphs:
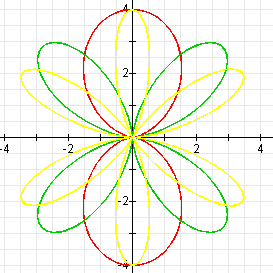
These graphs are the same as the graphs when a and b
are both positive, but they are rotated /k
radians.
Now let's consider the case where a is positive and b is negative. Let's let k be odd, and look at a few graphs. The equations
have the following graphs:
These graphs are the same as the graphs when a and b
are both positive, but they are rotated /k
radians.
Let's let k be even and consider the following graphs:
They look like
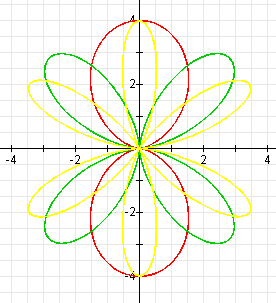
These graphs are the same as the graphs when a and b
are both positive, but they are rotated /k
radians.
Conclusions about the graph of the polar equation
when
k is the number of leaves of the rose.
The leaves are equally spaced about the origin.
The length of each leaf (the distance from the origin to the point farthest from the origin) is | a | + | b |.
When a and b are both positive, the end of one leaf is the point (0, | a | + | b | ).
When a and b are both negative and k is
odd, the graph is the graph when a and b are both positive rotated
/k radians.
When a and b are both negative and k is even, the graph is the same as the graph when a and b are both positive.
When a is negative, b is positive, and k is odd, the graph is the same as the graph when a and b are both positive.
When a is negative, b is positive, and k is
even, the graph is the graph when a and b are both positive
rotated /k radians.
When a is positive, b is negative, and k is
odd, the graph is the graph when a and b are both positive rotated
/k radians.
When a is positive, b is negative, and k is
even, the graph is the graph when a and b are both positive rotated
/k radians.