

![]()
Case 2:
![]()
As an example, let's consider the equation
![]()
Here is the graph:
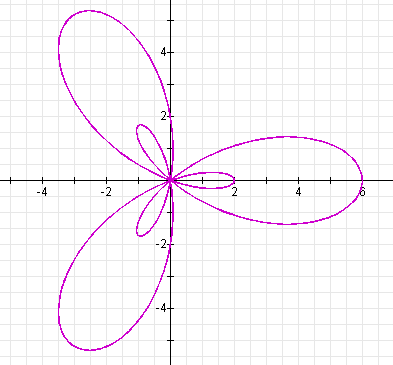
In this case, there are two sets of leaves: large leaves and small leaves. The number of large leaves and the number of small leaves is k. The length of the large leaves is | a | + | b |, and the length of the small leaves is | b | - | a |. In this example, k is odd, and the small leaves are inside the large leaves.
Let's see what happens when k is even.
The graph of the equation
![]()
is shown below
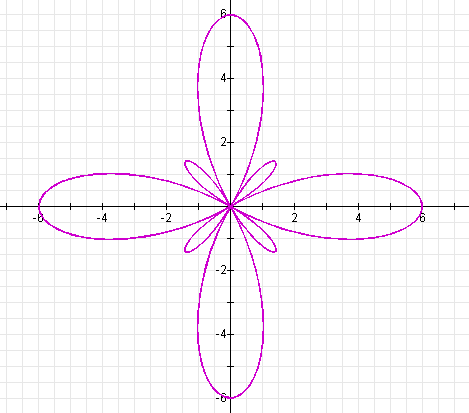
Again, there are k large leaves and k small leaves. The length of the large leaves is | a | + | b |, and the length of the small leaves is | b | - | a |. The difference between this example and the example when k is odd is that the small leaves are between the large leaves instead of inside the large leaves.
Let's consider an example when a and b are both negative, and k is odd, as in the following equation:
![]()
When we plot this equation on the same axes as the equation
![]()
we see that
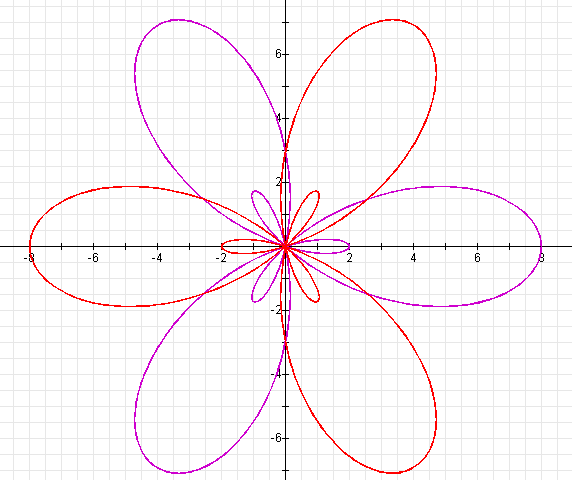
there are k large leaves and k small leaves.
The length of the large leaves is | a | + | b |, and the length of
the small leaves is | b | - | a |. The graph when a
and b are both negative, though, is the graph when a and b
are both positive rotated ![]() /k
radians.
/k
radians.
When a and b are both negative, and k is even, the graph is exactly the same as the graph when a and b are both positive. The graph of
![]()
looks like the following:
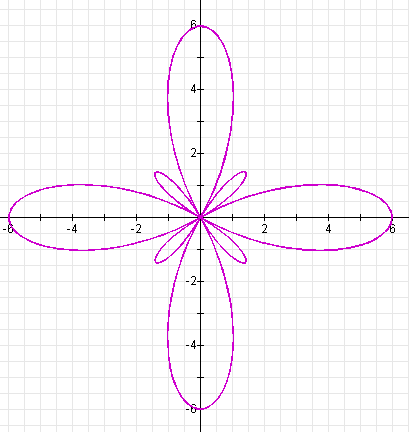
which is the same as the graph of
![]()
above.
Let's consider an example when a is negative, b is positive, and k is odd, as in the following equation:
![]()
The graph looks like the following:
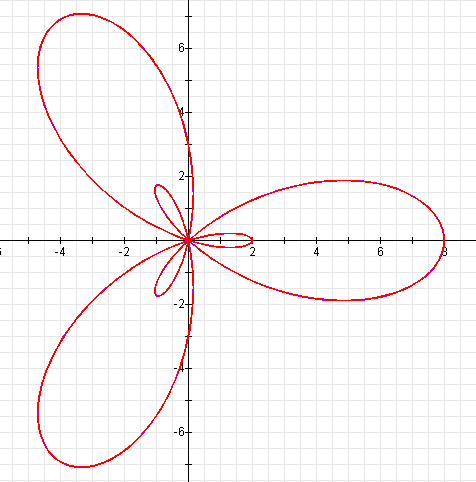
This graph is exactly the same as the graph when a and b are both positive, as in the above equation
![]()
Now let's consider an example where a is negative, b is positive, and k is even, as in the following equation:
![]()
The graph is the following:
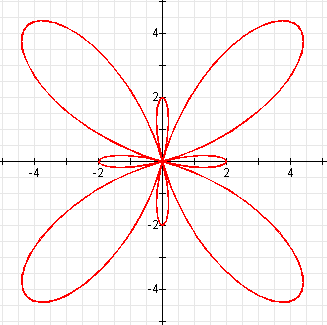
This graph is the same as the graph when a and b
are both positive, but it is rotated ![]() /k
radians.
/k
radians.
Finally, let's look at an example where a is positive and
b is negative. Regardless of whether k is even or odd, the
graph is the same as the graph when a and b are both positive, but
it is rotated ![]() /k
radians.
/k
radians.
For example, look at the graphs of the following equations:
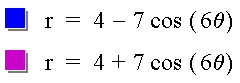
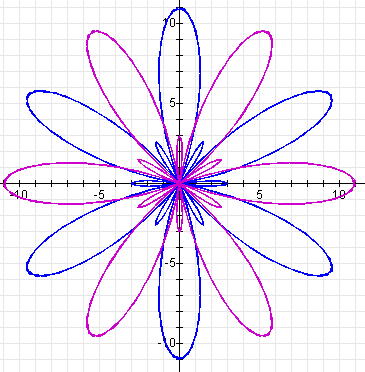
For an example when k is odd, look at the following:
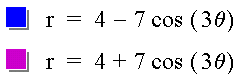
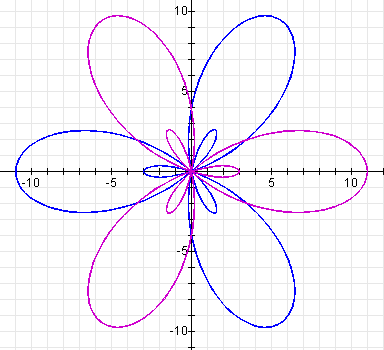
Conclusions about the graph of the polar equation
![]()
when
![]()
The rose has k large leaves and k small leaves.
The leaves are equally spaced about the origin.
The length of each large leaf (the distance from the origin to the point farthest from the origin) is | a | + | b |.
The length of each small leaf is | b | - | a |.
When a and b are both positive, the end of one small leaf and one large leave is on the positive x-axis.
When a and b are both negative and k is
odd, the graph is the graph when a and b are both positive rotated
![]() /k radians.
/k radians.
When a and b are both negative and k is even, the graph is the same as the graph when a and b are both positive.
When a is negative, b is positive, and k is odd, the graph is the same as the graph when a and b are both positive.
When a is negative, b is positive, and k is
even, the graph is the graph when a and b are both positive
rotated ![]() /k radians.
/k radians.
When a is positive, b is negative, and k is
odd, the graph is the graph when a and b are both positive rotated
![]() /k radians.
/k radians.
When a is positive, b is negative, and k is
even, the graph is the graph when a and b are both positive
rotated ![]() /k radians.
/k radians.