
In the equiangular spiral of the Nautilus or the snail-shell or Globigerino, the whorls continually increase in breadth, and so on in a steady and unchanging ratio.... It follows that the sectors cut off by successsive radii, t equal vectorial angles, are similar to one another in every respect and that the figure may be conceived as growing continuously without ever changing its shape the while.
Sir D'Arcy W. Thomson (1860-1948)
Archimedes, Leonardo, Newton-all very practical men, but with something more. A sense of wonder, perhaps...Very mysterious, very mysterious. And very exciting. That is the thing-excitement. You get it by being God, by constructing, and you get it by watching God, by observing things as they are.
J. L. Synge
In the brief anthology of the golden section, there is a beautiful curve which has not only been studied by mathematicians for hundred of years but has been represented in Nature for thousands of centuries not only in flora and in fauna but also in human embrio: the equiangular spiral.
The equiangular spiral has a lot longer history than the science of mathematics. The spiral has been produced for thousands of years in the shape of the nautulis shell, the arrangement of sunflower seeds in the sunflower, among various other natural phenomena.
The spiral has been known by a variety of names corresponding to one or another of its fetures. By Descartes, who discussed it in 1638, it was designated the equiangular spiral, because the angle at which a radius increasess in geometrical progression as its polar angle increasess in arithmetical progression, it has been called the geometrical spiral. Descartes started from the property s = a.r. Torricelli, who died in 1647, worked on it independently and used for a definition the fact that the radii are in geometric progression if th angles increase uniformly. From this he discovered the relation s = a.r; that is to say, he found the rectification of the curve. Halley noting that the lenghts of the segments cut off from a fixed radius by successive turns of the curve were continued proportion, named it the proportional spiral. Jacob Bernoulli (1654-1705), who was so fascinated by the mathematical beauty of the curve that he asked that it might be engraved on his tombstone, called it the logarithmic spiral. Bernoulli (1654-1705) who requested that the curve be engraved upon his tomb with the phrase "Eadem mutata resurgo" ("I shall arise the same, though changed.")
In more recent times, Rev. H. Moseley,
a Canon of Bristol Cathedral gave a simple, mathematical account
of the spiral shell. Even earlier, Sir Christopher Wren, considering
its architecture, perceived that the spiral was a cone coiled
about anaxis.
The fundamental mathematical property of the equiangular (or logarithmic) spiral corresponds precisely to the biolagical principle that governs the growth of the mollusk's shell. This principle is the simplest possible: the size increases but the shape is unaltered. The molusk's shell grows longer and wider to accommodate the growing animal, but the shell remains always similar to itself. It grows at one nd only, each increment of lenght being balanced by a proportional increase of radious so that its form is unchanged. The shell grows by accretion of material; more accurately, it accumulates rather than grows.
The only mathematical curve to follow this
pattern of growth is the logarithmic spiral. Because of this,
Bernoulli described it as spira mirabilis. Of course, the pattern
of development can be imitated by mathematical forms other than
this spiral. A rectangle, a paralleogram, a cone, etc. can grow
while remaining similar to itself in shape. This interested not
only in Greeks of 500 B.C. but also the Egyptians a thousand years
earlier.
Equiangular spiral (also known as logarithmic
spiral, Bernoulli spiral, and logistique) describe a family of
spirals. It is defined as a curve that cuts all radii vectors
at a constant angle.
Explaination:
1. Let there be a spiral (that is, any
curve ![]() where f is a monotonic inscreasing function)
where f is a monotonic inscreasing function)
2. From any point P on the spiral, draw a line toward the center
of the spiral. (this line is called the radial vector)
3. If the angle formed by the radial vector and the tangent for
any point P is constant, the curve is an equiangular spiral.
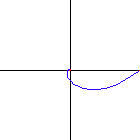
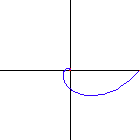
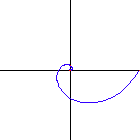
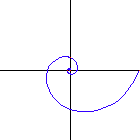
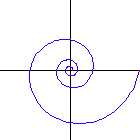
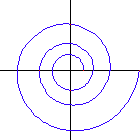
A special case of equiangular spiral is the circle, where the constant angle is 90 Degrees.
Equiangular spiral with 40, 50, 60, 70,
80 and 85 degrees. (left to right, top to bottom)
 |
 |
 |
 |
 |
 |
|
|
||
Let alpha be the constant angle.
Parametric: {E^(t Cot[alpha]) Cos[t], E^(t
Cot[alpha]) Sin[t]}
Cartesian: x^2 + y^2 == E^(ArcTan[y/x] Cot[alpha] )
Polar: r == E^(theta Cot[alpha])
Pedal: p == r Sin[alpha]
Whewell: r == s Cos[alpha]
Cesaro: rho == s Cot[alpha]
The equation of Equiangular (or logarithmic spiral in Polar Coordinates is given by
where r is the distance from the Origin, is the angle from the x-Axis, and a and b are arbitrary constants. It can be expressed parametrically using
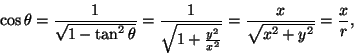
which gives

The logarithmic spiral can be constructed
from equally spaced rays by starting at a point along one ray,
and drawing the perpendicular to a neighboring ray. As
the number of rays approached infinity, the sequence of segments
approaches the smooth logarithmic spiral.
For a discussion Click Here
The rate of change of Radius is
and the Angle between the tangent and radial line at the point
is
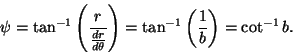
So, as
![]()
![]() and the spiral approaches a Circle.
and the spiral approaches a Circle.
If P is any point on the spiral, then the length of the spiral from P to the origin is finite. In fact, from the point P which is at distance r from the origin measured along a Radius vector, the distance from P to the Pole along the spiral is just the Arc Length. In addition, any Radius from the origin meets the spiral at distances which are in Geometric Progression.

The Arc Length, Curvature, and Tangential Angle of the logarithmic spiral are
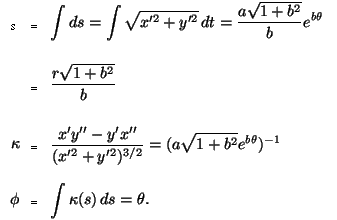
The Cesàro Equation, An Intrinsic
Equation which expresses a curve in terms of its Arc Length s
and Radius of Curvature R (or equivalently, the Curvature ![]() ,
,
Click Here to see Pursuit, radial, evolute, negatives pedal, pedal, caustic, parallel and inversion curves of Equiangular (or Logarithmic Spiral)
There is a close relation between the golden ratio (or known as divine proportion) and the Equiangular Spiral. In particular, an Equiangular Spiral can be derived from a golden rectangle and a golden triangle. For details of these relationships, Please Click on the following links:
|
|
|
|
|
|
|
|
1. http://www.best.com/~xah/SpecialPlaneCurves_dir/EquiangularSpiral_dir/equiangularSpiral.html
2. www.treasure-troves.com/math/logarithmicspiral.html
3. H S M Coxeter's Introduction to Geometry, published by Wiley, in its Wiley Classics Library series, 1989
4. Huntley, H.E. The Divine Proportion: A Study in Mathematical Beauty. 1970, DoverPub., New York
This page created November 26, 1999
This page last modified December 4, 1999