Ken Montgomery

EMAT 6690

INSTRUCTIONAL UNIT: Distance, Area, and Volume

Distance

Perimeter

Area

Surface Area

Volume

PERIMETER

Perimeter, the quintessential problem of farmers and fence-builders the world over, is the total distance around a polygon. The calculation of perimeter is relatively straightforward in that one must simply add all of the side lengths of the polygon. Consider the quadrilateral given in Figure 1.

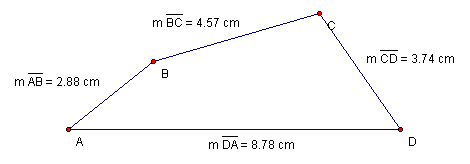
Figure 1: Quadrilateral ABCD

To find the perimeter of Quadrilateral ABCD, we simply add the lengths of the four sides (Equation 1).

Equation 1:

This definition may be applied to all n-gons (polygons with n sides) regardless of whether or not they are regular. A regular polygon has all sides congruent (of equal measure). However, in the case of regular polygons, the number of sides, n may be multiplied by the side-length. Consider the regular hexagon in Figure 2.

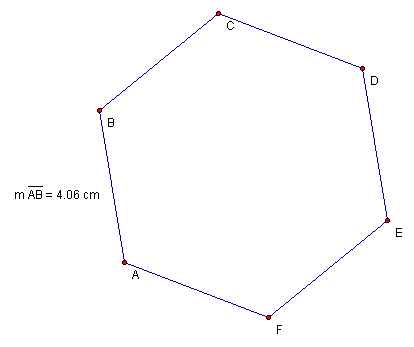
Figure 2: Regular Hexagon ABCDEF

Notice that we are only given one side-length, . However, since Figure 5 is a regular hexagon, all six sides are congruent, so we multiply the side-length by 6 to find the perimeter (Equation 2).

Equation 2:

Sometimes, both addition and multiplication may be used in calculating perimeter, such as in the case of parallelograms, which have two pairs of congruent, opposite sides (Figure 3).

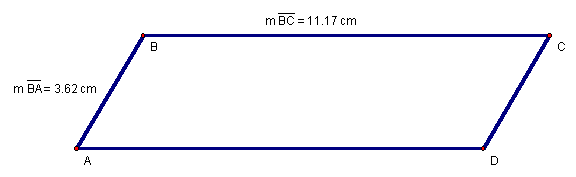
Figure 3: has opposite sides congruent

To find the distance around , we need only recognize that and, thus the perimeter is given in Equation 3.

Equation 3:

Circumference

Analogous to perimeter, for polygons, the distance around a circle is known as the circumference. The distance from the center of the circle to any point on the circle is called the radius. The radius is a constant value, since a circle, by definition, is a locus of points equidistant from a given point (the center). The diameter is twice the value of the radius (Equation 4).

Equation 4:

The ratio of circumference to diameter is constant for any circle, regardless of the size of the radius. This constant is known as pi, represented by the Greek letter (), and is approximated in the below relation.

By definition therefore, the valueis equal to this ratio of circumference and diameter (Equation 5).

Equation 5:

Multiplying both sides of the equation by d yields Equation 6.

Equation 6:

Substituting from Equation 4, we also have Equation 7.

Equation 7:

There are thus, two convenient formulas for circumference calculation depending upon whether the diameter or radius is indicated.

Return to EMAT 6690