
Ken Montgomery
EMAT 6690
INSTRUCTIONAL
UNIT: Distance, Area, and Volume
VOLUME
Like its two-dimensional cousin, the square, which (with side-length one) represents the unit measure of area, the cube (with side-length one) represents the unit measure of volume (Figure 1).
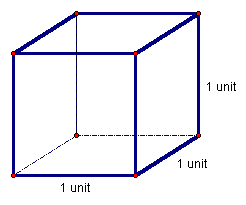
Figure 1: A cube with side-length 1 unit
A cube is a special type of solid known as a prism and in a cube,
with side
length, s, there are![]() ,
one-unit cubes (Figure 2).
,
one-unit cubes (Figure 2).
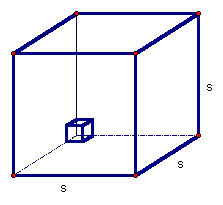
Figure 2: A cube with side-length, s
The volume formula for a cube is therefore given in Equation 1.
Equation 1:![]()
Rectangular Prism
The volume of a rectangular prism (Figure 3) likewise may be thought of as the number of unit cubes that it would contain.
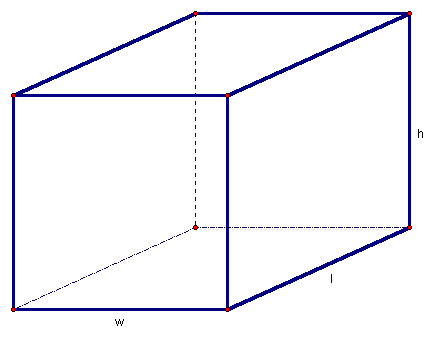
Figure 3: Rectangular prism with dimensions length (l), width (w) and height (h)
The volume, or number of unit-cubes contained in the rectangular prism of Figure three is equal to the product of its three dimensions, length, width and height, in terms of those same units (Equation 2).
Equation 2:![]()
We next consider an important principle, necessary to generalize certain formulas.
Consider the maximization problem of finding the greatest volume for a box (rectangular prism). Although calculus could be applied to find a solution, one may also explore possible solutions via trial and error or by constructing a spreadsheet. Open MaxBox.gsp to explore the nature of this problem and construct a spreadsheet to display values for different side lengths that would determine the volume.
Cavalieriís Principle
The volumes of two objects are equal, if the heights of the two
objects are
equal and if the cross-sectional areas are equal at every level.
Pyramid
The general formula for a pyramid is given in Equation 3.
Equation 3: ![]()
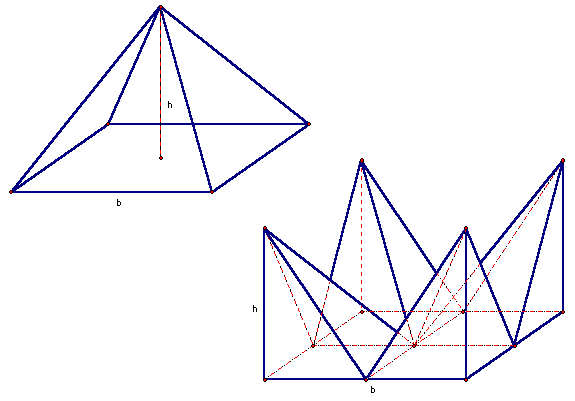
Figure 4: A square pyramid, divided into four congruent right pyramids and rearranged
To validate Equation 3, consider the square pyramid in Figure 4. A total of eight additional congruent, right pyramids would be necessary to create the rectangular prism, whose volume is equal to the product of its base and height. Because of Cavalieriís Principle, the formula in Equation 3 applies to all pyramids.
Open Pyramid.gsp or PyramidBox.gsp to investigate the volume calculation of a square pyramid.
Cone
Cones differ from pyramids primarily, in that the base is a circle. The surface bounding the volume of the cone, between the non-planar vertex and the base is therefore continuous. The relationship between a cone and cylinder of the same base and height (Figure 5) is the same as the relationship between a pyramid and a prism of the same base and height.
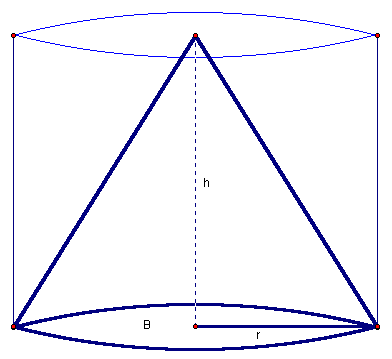
Figure 5: Cone
with base, B,
radius, r and height, h
The Volume of a pyramid is given by Equation 4, where B is the area of the base and h is the height.
Equation 4: ![]()
As we have seen previously, the area formula for a circle can be derived from the area of a polygon with n-sides, as n approaches infinity. To derive the formula for a cone therefore, we consider a pyramid with a polygonal base of n sides (an n-gon). The area of this n-gon is equal to B and if we allow n to approach infinity, the n-gon becomes circular and we have its area given in Equation 5.
Equation 5: ![]()
Substitution for B yields the volume formula for a cone.
Equation 6: ![]()
We next explore the concept of volume within the context of solids
with
fewer flat surfaces and right angles.
Sphere
A sphere is the three-dimensional extension of a circle. Whereas a circle is all points in a plane, equidistant from a single point, a sphere is all points in space equidistant from a single point, and as with its cousin the circle, that distance is referred to as the radius, r (Figure 6).
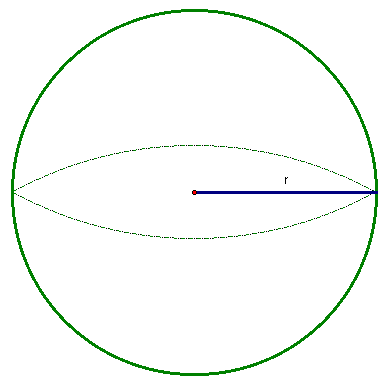
Figure 6: Sphere with radius r
The volume of a sphere is given in Equation 7 and can be derived either using calculus. However, we shall derive the formula here, from the volume of a pyramid.
Equation 7: ![]()
Given the formula for the volume of a pyramid Equation 8, we can consider a sphere to consist of n, pyramids with a common vertex.
Equation 8: ![]()
One such pyramid is illustrated in Figure 7.
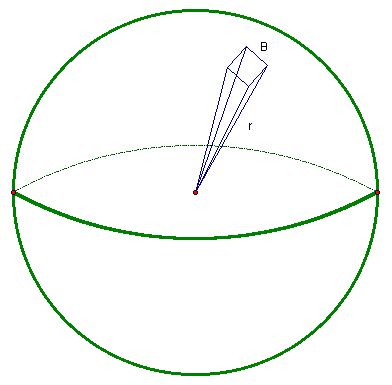
Figure 7: A sphere comprised of pyramids with base B and height, r
To find the total volume of the sphere, we thus find the total volume of the n, pyramids (Relation 9).
Relation
9: ![]()
Rewriting relation 9, via the associative and commutative properties yields Relation 10.
Relation 10: ![]()
Relation 10 represents an approximation of the total volume, where the product nB is an approximation of the surface area of the sphere. The product is an approximation because it represents the sum of n flat surfaces, B. However, we know the exact surface area of the sphere, which nB approximates, as n approaches infinity. The formula for the surface area of a sphere provides this value (Equation 11).
Equation 11: ![]()
Substituting from Equation 11, for the product nB, we obtain Equation 12.
Equation 12: ![]()
Simplifying Equation 12, yields the volume formula for a sphere (Equation 13).
Equation 13: ![]()
Lastly, we consider the volume of a cylinder.
Cylinder
A right cylinder is shown in Figure 8.
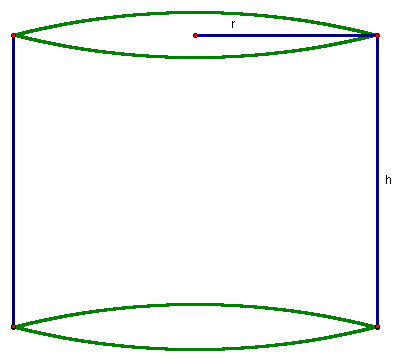
Figure 8: Cylinder with height, h
The generalized volume of any prism, to which Cavalieriís principle applies is given in Equation 14.
Equation 14:![]()
For the case of a cylinder, the base is a circle and we thus obtain the formula for the volume of a cylinder (Equation 15).
Equation 15: ![]()
Return to EMAT 6690