
Ken Montgomery
EMAT 6690
INSTRUCTIONAL
UNIT: Distance, Area, and Volume
AREA
Area is the measure of an enclosed region, which (in plane Euclidian geometry) lies in the Euclidian plane. Sometimes we think of this enclosed region as a “covering.”
Having explored distance in the context of two-dimensions, we now turn our attention to the next two-dimensional measure, area, which requires both dimensions length and width. We will first explore this concept within the context of triangles, then quadrilaterals (four-sided figures) and finally, regular polygons.
Triangles
The area of a triangle is given by the product of one-half of a base and the corresponding height (Equation:1).
Equation 1: ![]()
Since the altitude is involved in this formula, to derive the general area formula for a triangle, there are three cases that must be considered: altitude as a side of the triangle, altitude inside of the triangle and altitude outside the triangle.
Case 1: Altitude as a side of the triangle
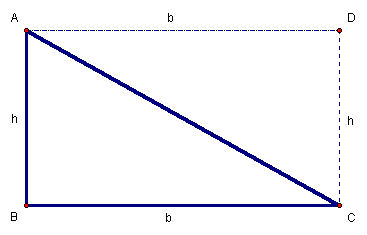
Figure 1:
Rectangle ABCD,
with![]()
Given ![]() ,
we construct Rectangle ABCD, with side lengths b
and h. Since Rectangle ABCD, is a parallelogram, we
have Equation
2.
,
we construct Rectangle ABCD, with side lengths b
and h. Since Rectangle ABCD, is a parallelogram, we
have Equation
2.
Equation 2: ![]() and
and![]()
From the definition of congruence, we have Equations 3 and 4.
Equation 3: ![]()
Equation 4: ![]()
From the transitive property, we have Equation 5.
Equation 5:![]()
By the Side-Side-Side Triangle Congruence Postulate (SSS), we have Equation 6.
Equation 6: ![]()
Since the area of a region is equal to the sum of the areas of its parts, we have Eqution 7.
Equation 7: ![]()
We then substitute and have Equation 8.
Equation 8:![]() .
.
The distributive property yields Equation 9.
Equation 9: ![]()
We apply the area formula of a rectangle (Equation 10).
Equation 10: ![]()
Substitution yields Equation 11.
Equation 11: ![]()
From the division property, we have Equation 12, the area formula for the right triangle.
Equation 12: ![]()
We next consider the case for area of a triangle, when the altitude is on the interior of the triangle.
Case 2: Altitude inside the triangle
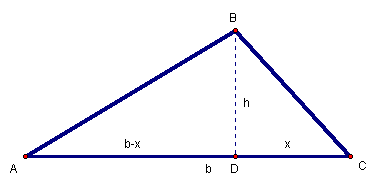
Figure 2: ![]() with
interior altitude
with
interior altitude
Given ![]() ,
construct the altitude,
,
construct the altitude, ![]() (Figure 2). The base,
b, of
(Figure 2). The base,
b, of![]() is
now divided into two segments,
is
now divided into two segments, ![]() and
and![]() .
The measure of the base is given by Equation 13.
.
The measure of the base is given by Equation 13.
Equation 13: ![]()
We define the length of![]() to
be the arbitrary measure, x and thus obtain
Equation 14.
to
be the arbitrary measure, x and thus obtain
Equation 14.
Equation 14: ![]()
The area of ![]() is
equal to the sum of the areas of
is
equal to the sum of the areas of ![]() and
and![]() (Equation
15), by the Area Addition Postulate.
(Equation
15), by the Area Addition Postulate.
Equation 15: ![]()
Both triangles, ![]() and
and![]() are
right triangles, so by application of the formula from
Case 1, we have Equation 16.
are
right triangles, so by application of the formula from
Case 1, we have Equation 16.
Equation 16: ![]()
Simplifying via the distributive property yields Equation 17.
Equation 17: ![]()
Simplification again yields the triangle area formula, for interior altitude (Equation 18):
Equation 18: ![]()
Case 3: Altitude outside the triangle
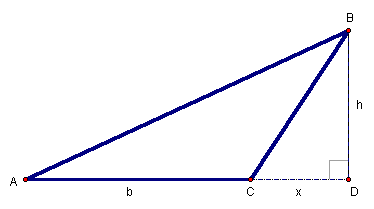
Figure 3: ![]() with
exterior altitude
with
exterior altitude
Given ![]() ,
we extend
,
we extend![]() to
the point D and construct the altitude,
to
the point D and construct the altitude, ![]() (Figure 3). Now,
whereas we were concerned with the sum of two triangles in Case 2, we
are now
concerned with the difference between two triangles. With the length of
(Figure 3). Now,
whereas we were concerned with the sum of two triangles in Case 2, we
are now
concerned with the difference between two triangles. With the length of
![]() arbitrarily
defined as x. We thus have the measure of
arbitrarily
defined as x. We thus have the measure of![]() given
by Equation 19, with the individual measures given by
Equations 20 and 21.
given
by Equation 19, with the individual measures given by
Equations 20 and 21.
Equation 19: ![]()
Equation 20: ![]()
Equation 21: ![]()
The area of the right triangle, ![]() is
given by Equation 22.
is
given by Equation 22.
Equation 22: ![]()
Solving Equation 22 for![]() ,
we obtain Equation 23.
,
we obtain Equation 23.
Equation 23: ![]()
Since both triangles,![]() and
and![]() are
right triangles, we again apply Equation 12 from Case 1
to obtain Equation 24.
are
right triangles, we again apply Equation 12 from Case 1
to obtain Equation 24.
Equation 24: ![]()
Simplifying via the distributive property yields Equation 25.
Equation 25: ![]()
Simplifying via the associative property, we thus obtain the formula for the obtuse triangle (Equation 26).
Equation 26: ![]()
Heron’s Formula
Alternatively, area can be calculated using only the side lengths of the triangle via Heron’s Formula.
Having established the area formula for triangles, we next examine quadrilaterals.
Quadrilaterals
A quadrilateral is a two-dimensional shape, with four sides. Classification of quadrilaterals and inheritance of quadrilateral properties is illustrated in Figure 4.
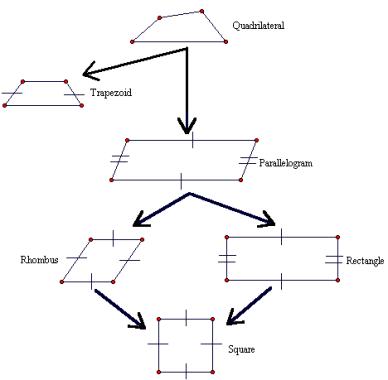
Figure 4: Classification and progression of quadrilaterals
Shared properties of quadrilaterals are illustrated in Figure 5.
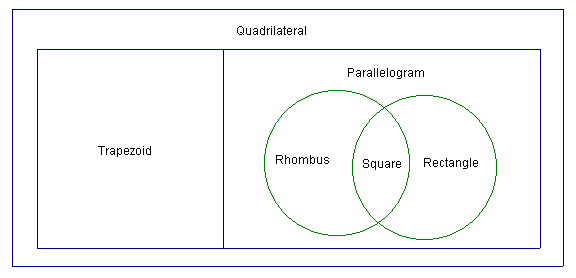
Figure 5: Venn Diagram of quadrilaterals
Trapezoid
A trapezoid is a quadrilateral with one pair of sides parallel (Figure 6).
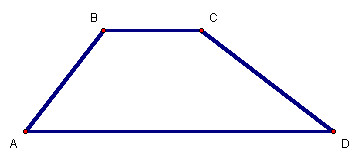
Figure 6: Trapezoid ABCD
To find the area of a trapezoid, we need to know the height of the
trapezoid
and the lengths of the two parallel sides (bases), so we drop a
perpendicular
segment,![]() from B to
from B to ![]() and measure the
lengths of
and measure the
lengths of ![]() ,
,![]() and
and ![]() (Figure 7).
(Figure 7).
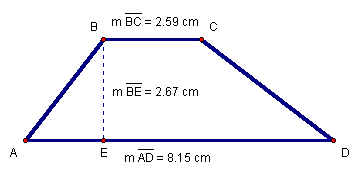
Figure 7: Trapezoid ABCD with measures
The area of the Trapezoid is given in Equation 27.
Equation 27: ![]()
Substituting the values from Figure 7, we have the solution given in Equation 28.
Equation 28: ![]()
The area formula for a trapezoid can be derived from the area formula for a triangle, restated here in Equation 29.
Equation 29: ![]()
We can create a trapezoid by truncating a triangle (Figure 8).
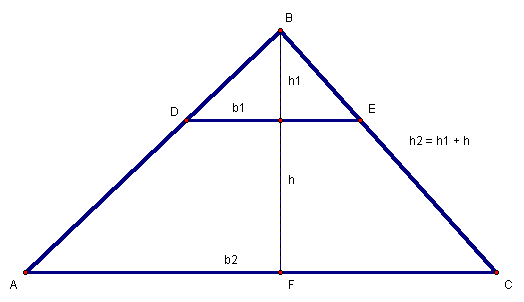
Figure 8: ![]() and
and![]() are
similar triangles
are
similar triangles
Beginning with![]() ,
we construct
,
we construct![]() parallel
to
parallel
to![]() and
drop the perpendicular
and
drop the perpendicular![]() .
Since
.
Since ![]() have
have![]() by
AAA similarity which yields Equation 30, where
by
AAA similarity which yields Equation 30, where![]() is
the height of
is
the height of![]() and
is defined in Equation 31.
and
is defined in Equation 31.
Equation 30:![]()
Equation 31:![]()
The area of Trapezoid AEDC is equal to the difference of the two similar triangles (Equation 32) and is displayed in Figure 9.
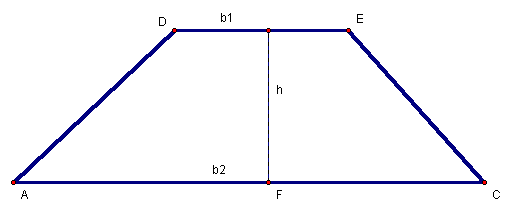
Figure 9: Trapezoid ADEC as the difference of two triangles
Equation 32: ![]()
Substituting the triangle area formula (Equation 26), we have Equation 33.
Equation 33: ![]()
Substitution from Equation 31 then yields Equation 34.
Equation 34: ![]()
Applying the distributive property, we have Equation 35.
Equation 35: ![]()
Clearing fractions in Equation 30 yields Equation 36.
Equation 36: ![]()
Substituting from Equation 36 and Equation 31 gives Equation 37.
Equation 37: ![]()
Distributing again yields Equation 38.
Equation 38: ![]()
Cancellation of terms simplifies the relationship to Equation 39.
Equation 39: ![]()
Factoring out the common terms yields thus yields the formula for the area of the trapezoid (Equation 40).
Equation 40: ![]()
Open the TrapezoidArea.gsp file to compare the value of this formula with Sketchpad’s computed area. Click on the point, D and drag it up. What happens?
There is also a reciprocal relationship between the Trapezoid and Triangle, area formulas.
Notice what happens when we let ![]() approach
0 (Figure 10). We see that Trapezoid ABCD becomes
approach
0 (Figure 10). We see that Trapezoid ABCD becomes ![]() .
Substituting 0 for
.
Substituting 0 for ![]() in
Equation 40, we have the simplified formula in Equation
41.
in
Equation 40, we have the simplified formula in Equation
41.
Equation 41: ![]()
Since we no longer have two bases, we drop the subscript from![]() and
have the formula for the area of a triangle in Equation
42.
and
have the formula for the area of a triangle in Equation
42.
Equation 42: ![]()
Compare Trapezoid ABCD (Figure 10) and ![]() in
Figure 11.
in
Figure 11.
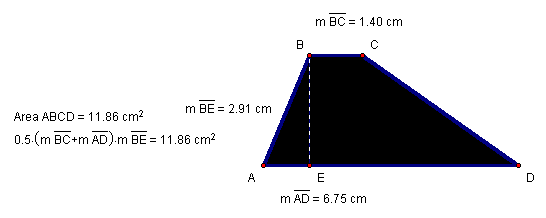
Figure 10: Trapezoid ABCD with measured and calculated areas
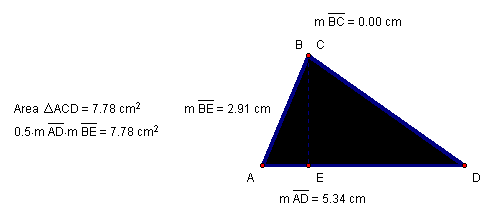
Figure 11: ![]() with
measured and calculated areas
with
measured and calculated areas
Open the Trap2Tri.gsp file in Sketchpad,
click on
![]() and
drag this segment to the left, until points B and C are
coincident and
and
drag this segment to the left, until points B and C are
coincident and![]() .
Then measure the area of
.
Then measure the area of ![]() and
calculate the area via the formula.
and
calculate the area via the formula.
Parallelogram
Every parallelogram can be divided into two congruent triangles by constructing the diagonal. Previously, we calculated the perimeter of a parallelogram. The formula for the area of a parallelogram is given in Equation 43, requiring only the measures of base and height.
Equation 43: ![]()
We calculate the area in Figure 12, after dropping perpendicular![]() and
measuring both
and
measuring both![]() and
and![]() .
.
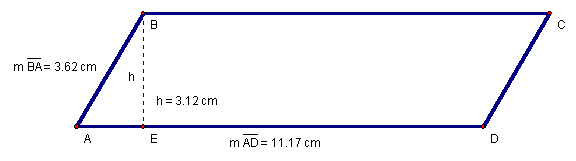
Figure 12: ![]() ,
with height and base measurements.
,
with height and base measurements.
From Equation 43, we substitute values from Figure 12 and obtain Equation 44.
Equation 44: ![]()
Open Parallelogram.gsp to verify the equivalency between sketchpad’s measured area and out calculated area for different parallelograms.
Notice what would happen, if we constructed diagonal ![]() .
.
![]() would
be divided into two congruent triangles:
would
be divided into two congruent triangles: ![]() and
and![]() .
The triangles are congruent because they have congruent
bases (b) and heights (h). Thus, the area of the
parallelogram is
given by Equation 45.
.
The triangles are congruent because they have congruent
bases (b) and heights (h). Thus, the area of the
parallelogram is
given by Equation 45.
Equation 45:![]()
The next quadrilateral that we investigate is a parallelogram with all right angles.
Rectangle
Recall that the rectangle (Figure 13) is a specialized case of the parallelogram (a parallelogram with right angles).
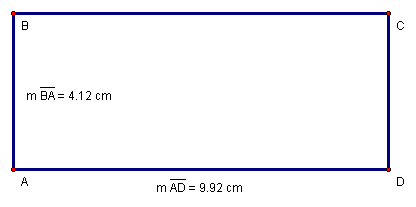
Figure 13: ![]()
The formula for the area of a rectangle (Equation 46) is simply an alternate statement of Equation 43, where the width (w) is equal to the height (h) and the length (l) is equal to the base (b).
Equation 46: ![]()
We calculate the area of![]() in
Equation 47 using the values from Figure 13.
in
Equation 47 using the values from Figure 13.
Equation 47: ![]()
Investigate the area of a rectangle by opening Rectangle.gsp.
Another special type of parallelogram does not necessarily have any
right
angles, but does have four congruent sides.
Rhombus
A rhombus (Figure 14) is a parallelogram with all sides congruent (equal in measure).
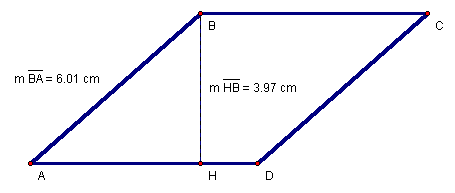
Figure 14: Rhombus ABCD
A rhombus is a parallelogram because it has opposite sides parallel and since all sides are congruent, it has opposite sides congruent. Since a rhombus is a parallelogram, it inherits all of the properties of a parallelogram including the area formula (Equation 46). To find the area of the rhombus in Figure 14, we simply find the product of the base and height (Equation 48).
Equation 48: ![]()
Open Rhombus.gsp to investigate the area properties and to test the application of the parallelogram formula for various rhombi. As can be seen in Figures 4 and 5, a rhombus can also be a rectangle.
Square
A square is both a rhombus and a rectangle. A square is a rhombus because it is a parallelogram with all four sides congruent and it is a rectangle because it is a parallelogram with four right angles. The square, therefore inherits the properties of rhombus and rectangle including the area formulas.
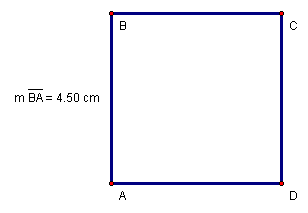
Figure 15: Square ABCD
One could use the area formula for a parallelogram (Equation 43), however since the base is equal to the width and the height is equal to the length, we may also use the formula for the area of a rectangle (Equation 46). Nevertheless, since length is also equal to width, we will always find the product of a number and itself, so we have the area of a square given by Equation 49, where s is the side length.
Equation 49: ![]()
To calculate the area of the square in Figure 15, we substitute the value of the side length (Equation 50).
Equation 50: ![]()
Open Square.gsp to investigate the area
calculation.
Brahmagupta's Formula
Analagous to Heron's
Formula, one may also calculate the area of a quadrilateral using Brahmagupta's
Formula.
As an extension of the application of the triangle area formula, we next consider the areas of regular polygons.
Regular Polygons
A polygon is a two-dimensional, geometric figure, with three or more sides. Triangles and quadrilaterals are all examples of polygons. A regular polygon is one in which all sides are congruent. Equilateral triangles and squares are both examples of regular polygons. Consider the regular hexagon (6-sided polygon) in Figure 16.
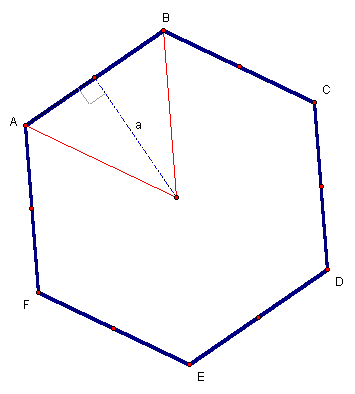
Figure 16: A
regular hexagon
There are six congruent, isosceles, right triangles in a regular hexagon. The total area is equal to the sum of the areas of the six triangles. The height of the triangle is the apothem, a (Figure 16), which yields Equation 56, from the area formula for a triangle.
The area of the regular n-gon (a polygon with n sides) is equal to the product of the area of one triangle and the total number of triangles (n) of the n-gon. Let a represent the apothem and s represent the side length. If the side is considered the base of the triangle and the height as the apothem, a, then the area for the regular polygon is should follow from Equation 51.
Equation 51: ![]()
Removing parentheses and applying the commutative property of multiplication, we obtain Equation 52.
Equation 52: ![]()
Application of the associative property of multiplication results in Equation 53.
Equation 53: ![]()
Recalling that the generalized perimeter of the regular hexagon is the product of the side length and the number of sides, since all sides are congruent, we have Equation 54.
Equation
54: ![]()
Substitution from Equation 54 into Equation 53 results in Equation 55.
Equation
55: ![]()
Open Hexagon.gsp to investigate one particular application of Equation 55.
The area of a regular polygon is given by Equation 56, where a, is the apothem (distance from the center to the midpoint of a side) and P is the perimeter.
Equation 56: ![]()
Using the result from Equation 56, we will derive the formula for the area of a circle.
Circle
The area for a circle can be derived from the area of a polygon, with n sides (an n-gon). As the number of sides, n, approaches infinity, the n-gon approaches the shape of a perfect circle (Figure 17).
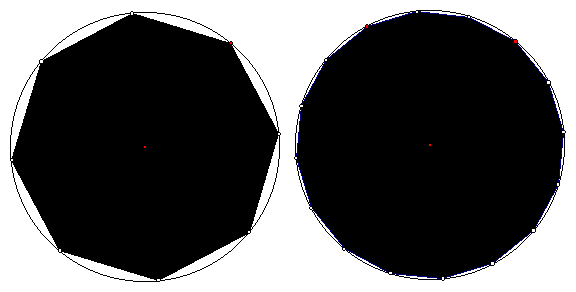
Figure 17: The shape of a polygon approaches the shape of a circle
As n approaches infinity therefore, the apothem, a, approaches the value r (radius of the circle) and the perimeter, P, approaches the circumference (Equation 57).
Equation 57: ![]()
Substituting circumference for perimeter and radius for apothem, we have (Equation 58).
Equation 58: ![]()
Simplifying this equation yields the area for the circle given in Equation 59.
Equation 59: ![]()
To investigate the areas for circles and their relation to the value
![]() ,
open CircleAreas.gsp.
,
open CircleAreas.gsp.
An important extension of area in plane geometry is the measure of
surface
area in solid geometry.
Return to EMAT 6690