The function of 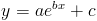
In this assignment we will have a look at the exponential function, there are a few things to note when looking at this function: firstly there are four constant values or constants, and two variables. The constants are a,b,c and e where e is Eulers constant which is roughly equal to 2.7. Thoughout this investigation the constants' values will be changed (all except e of course which will remain unchanged) which in turn with x, influence the output or y-value of the function.
The exponential function is often used with models of growth or decay
GROWTH:
The image below shows how exponentiality can be used to illustrate the exponential growth of populations (y axis) over time (x-axis):
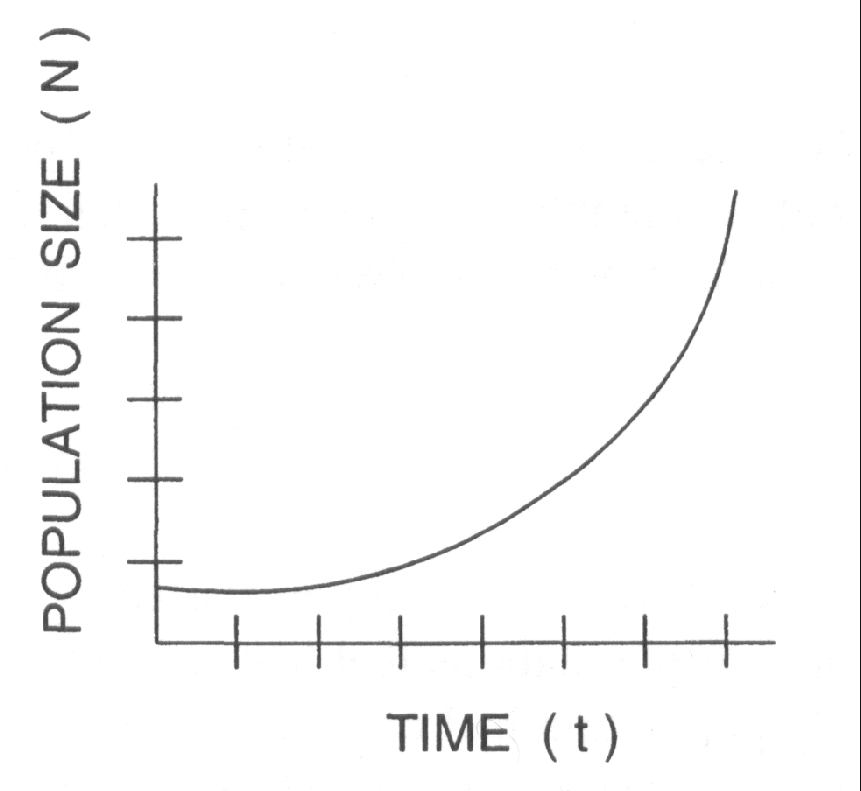
Figure 1: Exponential growth
DECAY:
Figure 2 shows the radioacive decay of an element with an annual decay of 10%. The formula is as follows for an initial weight of 200 grams:
![]()

Figure 2: Exponential decay
First lets look at the standard form of the exponential function with
a = 1, b = 1 and c = 1:
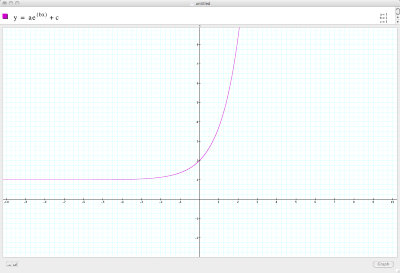
Reducing the values of a and b to zero yields a rather trivial function of y = c. Let's look at a few examples for different values of c:
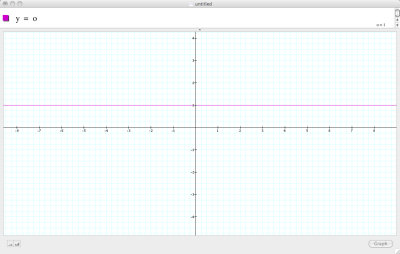
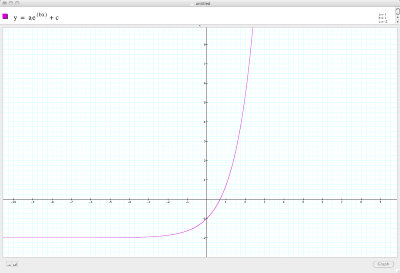
y = 1 (above)
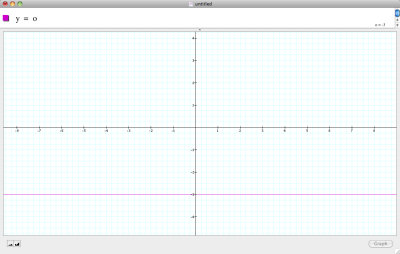
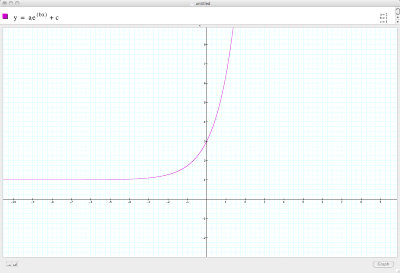
y = -3 (above)
From these function is it easy to see the purpose of the constant c which is that the entire graph is translated up or down in the corresponding units of c i.e. c = 3 would translate a graph up by three unit where c = -2 would translate is it downwards two units.
Different values of c applied:
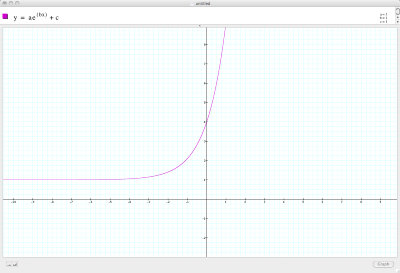
Applying this to the original function of a = 1, b = 1, c = 1

Compared to: a = 1, b = 1, c = 2
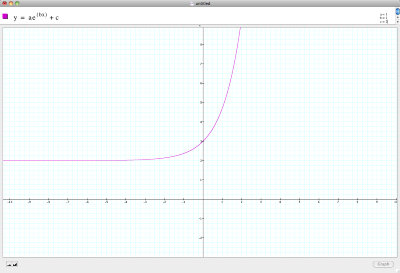
Function translated up by one unit.
And now: a = 1, b = 1, c = 3
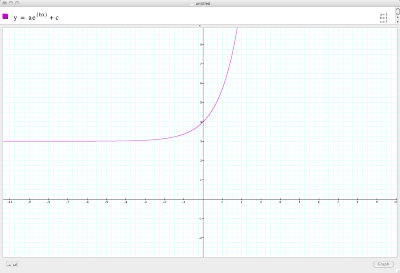
Function translated up by two units.
And similarly: a = 1, b = 1, c = -1
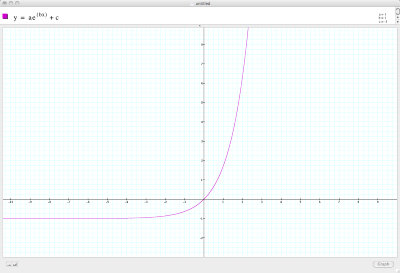
Function translated down by two units.
Lastly: a = 1, b = 1, c = -2
Function translated down by three units.
The effect of the constant a:
Let us compare the outcome of the function (the result if we were to substitute x for some value) for a = 1 and a = 20. If x is 5 then we get either
![]() = 148 (rounded
to 0 decimal points)
= 148 (rounded
to 0 decimal points)
or
![]() = 2986
(rounded to 0 decimal points)
= 2986
(rounded to 0 decimal points)
So the effect is that the range of is affected(accelerated/decelerated) in a linear way by the value of a. In other words y is simply magnified/shrunk by a factor of a.
Let's look at some examples:
a = 2, b = 1 and c = 1
The graph is now steeper than a = 1, but more specifically the y intercept is equal to c + a i.e. 1 + 2 = 3.
Here we have the same effect with a = 3, the graph is steeper still with a intercept of 1 + 3 = 4.
Similarly, for negative integer values of a, we get
y-intercepts = c + a i.e. 1 + (-2) = -1
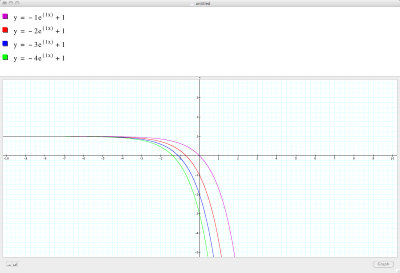
What is more interesting to note is what happens when is less than 1 but more than zero. In the following case four graphs are represented in the following way:

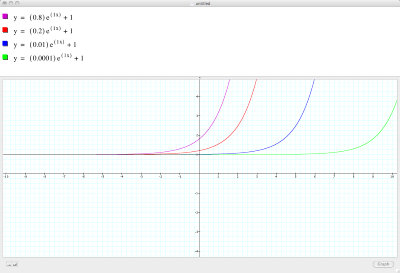
Here the graph is pulled closer to the horizontal asymptote with
x = log(y/a) for c = 0
The effect of the constant b:
The final constant in this investigation is b, from b's position in the equation we can see that it affects the function exponentially because of its linear multiplication on x. Compare the following graphs with the changes in a, where the effect was a linear acceleration, this constant b will result in an exponential acceleration/deceleration of the function (letting a = 1 and c = 1):

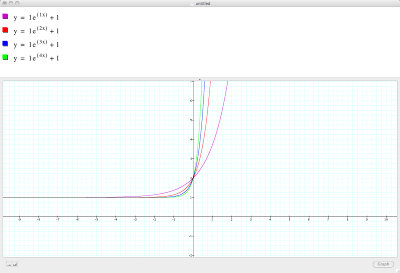
Notice that while the graph is much steeper, the y intercept has remained constant with the purple graph having a greater value than the green graph (higher value for b) when x is negative, but a smaller value after x becomes positive.
The mirror image(y axis reflection) can be seen by negating b:

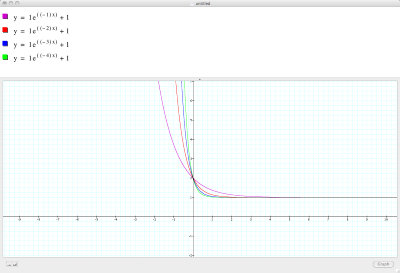
In closing, some combinations:
Finally let's see how this function can be manipulated using some different values for a,b and c:
Changing signs for a and b with c constant (1,1,1):

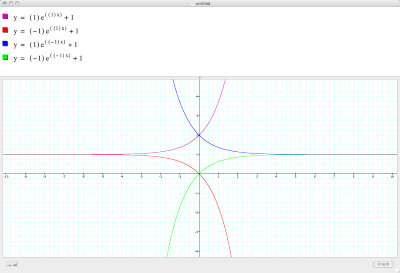
Values constant with changing signs (2,1,1):

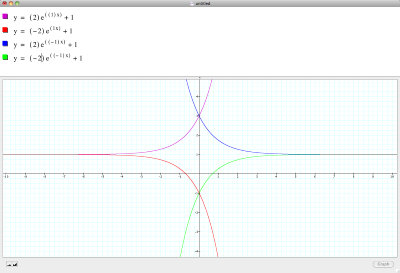
Values constant with changing signs (1,2,1):

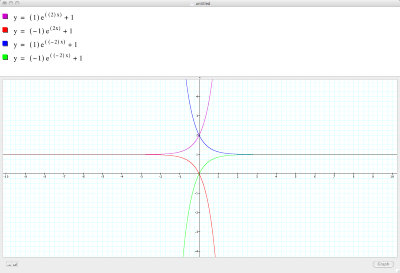
Values constant with changing signs (1,1,2):

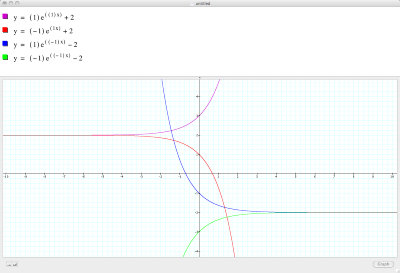
Same as above, ony c inverted (1,1,2):
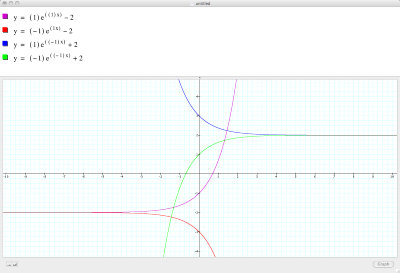
To end off, a quote:
The greatest shortcoming of the human race is our inability to understand the exponential function
- A. Bartlett, physicist
