The Golden Ratio
And it's geometrical
construction
December 10, 2010
We will construct introduce the golden ratio, geometric constructions and a construction of the ratio.
Please note: you might need a plugin to play the animations in this page.
1. The Ratio
1. The Golden Ratio
You can have a look at some applications(appearances) of the Golden Ratio in:
Here is the short version:
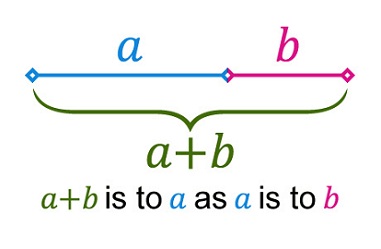
Or, by setting b = 1 and x = a we have:
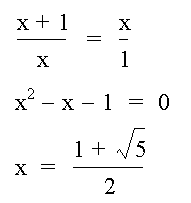
(We only take the
positive solution of the quadratic formula)
So to construct this we will need to
- find the root of 5
- add 1
- divide this sum by 2
For this we will need a few basics:
2. Constructions
Length
Before we can construct anything, we need a unit of measure: we need something we can call one. Any other number will then be defined in terms of this number 1.
In this video, we define 1 and then add 4 more units to itself, giving us a length of 5 in total:
Division and roots
Dividing by two is done simply by finding the midpoint of a line.
The root of a number can be constructed by adding one unit to its length, letting that new length be the diagonal of a circle and constructing a line perpendicular the diagonal through the point where the two line segments were added.
You can find an explanation of this construction here.
Now we just need to halve this length by finding the midpoint. Remember that this is the golden ratio as defined by the length of the unit we constructed at the very beginning of this investigation.
And that is how we can construct the golden ratio using only geometric construction.