Tangent circles

 November 13, 2010

This investigation has a look problems concerning circles and tangent circles. These types of problems are very rich in geometric concepts, and good for getting better understanding of geometric construction, proofs and relationships. We will be making use of Geometer SketchPad, you will need this application if you want to view the gsp file.

Please note: you might need a plugin to play the animations in this page.

1. The problem

2. Construction of the solution

3. Locus of all the solutions

4. Changing the locus

 

1. The problem

Given two circle, one inside the other. Find a circle that is tangent to both and also on the inside the bigger circle.

In other words, you are given:


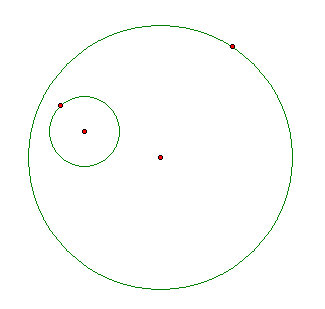
And you want to find:
Let's refer to the circles as small circle, big circle and tangent circle for the sake of simplicity (Just note that it is possible for the big circle to be smaller than the small circle and vice-versa, this naming convention is just used to keep it simple).

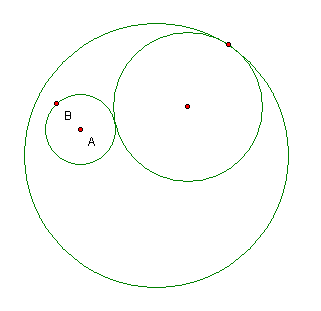
2. Construction of the solution

In solving this problem there are a few vital assumptions and constructions we'll be needing, also we will make these assumptions and finally work backwards from this solution to recreate it in Geometer SketchPad.

• Assumption: There are several solutions to this problem, i.e. several tangent circles that will satisfy the problem (like the blue circles in the figure below).

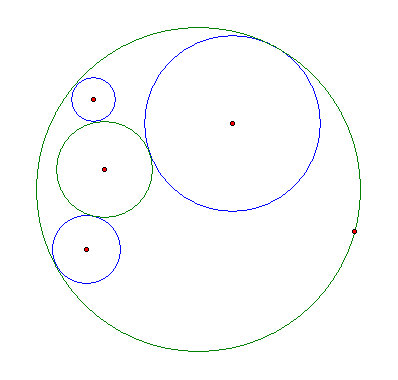
• For any solution (tangent circle), the exists a line though both its center and the big circle's center.  This is true because a line is uniquely determined by any two points (so we just let the two centers be those two points.)

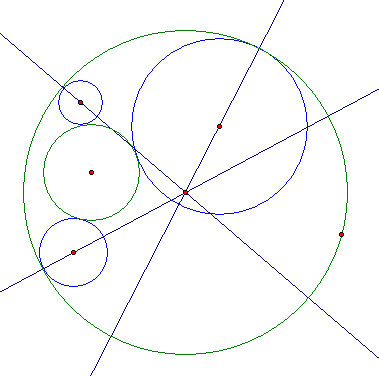
• The distance from any tangent circle to the center of the small circle is the radius of the small circle.

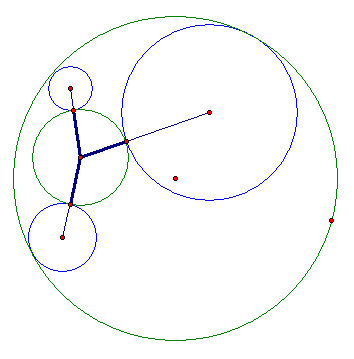
• The distance from the center of any tangent circle to both the small circle and the big circle must be it's radius by definition (it must be tangent to both circles).

• We can extend the tangent circle's radius by the radius of the small circle - the piont being to create an isosceles triangle that has an important property we will exploit to solve this problem.

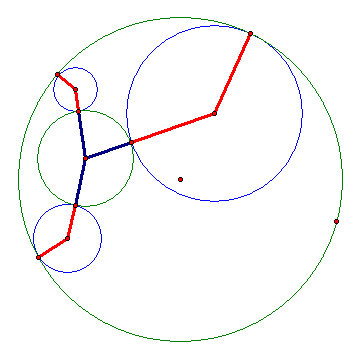
• We now have two equal lengths sharing the center point of the tangent circle.

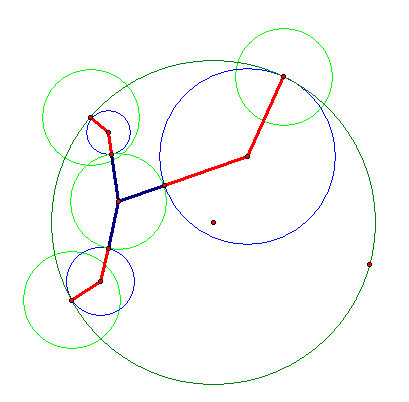
• The endpoints of these two lines are the sides of an isosceles triangle.  Now we can construct a perpendicular bisector of the base of this isosceles triangle. This bisecting line is vital to us because it contains all points that are of equal distance to both the small circle and the big circle.

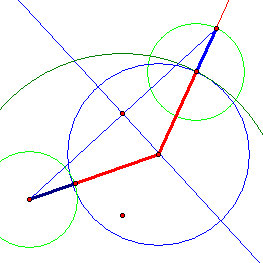
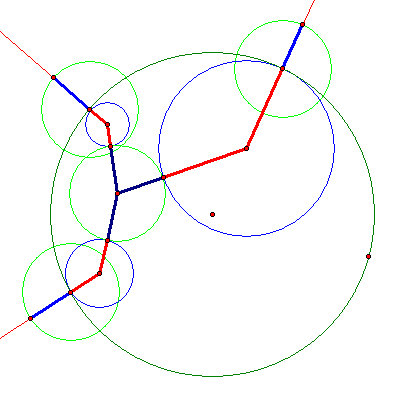
• Finally, we can now construct this is Geometer SketchPad:

• Have a look at how well this solution holds up when we change the size and location of both circles:

3. Locus of all possible solutions

If we move the point of tangency (to the big circle) and trace the center and the tangent circle, we get this:

4. Changing the locus

Using a special function in Geometer SketchPad, we can now see the locus of the center of tangent circle. Have a look at what kind of graph it is and also how it changes when the small circle exits the big circle.


The locus forms an ellipse around the center of the small and big circles and when the small circle exits the big circle we have a hyperbola.

In closing

The focus here was mainly on solving the problem of tangent circles but the last video was intended to show just a part of the wealth of mathematics that opens up once we have this solution. Feel free to have a look at the course page for lots more on tangent circles.