Orthocenters and Circumcircles
November 23, 2010
In this investigation we'll have a more in-depth look at orthocenters and circumcircles. The tools used are available for download through Assignment 5.Please note: you might need a plugin to play the animations in this page.
1. The Problem
3. Proof of the orthocenter conjecture
4. Proof of the circumcenter conjecture
1. The Problem
Here follows the construction of a triangle and then its orthocenter. This orthocenter is used to construct 3 new triangles and each of their respective orthocenters. After these constructions, the circumcircles are drawn for each triangle: the three colored ones and the main traingle as well.
2. Some Conjectures
It is important to note that just because something appears to be true does not make it necessarily true...
Here we have two specific instances of things that appear to be true:
- The orthocenter of each sub-triangle is a vertex of the main traingle.
- The circumcircles are equal in size.
The proof of each conjecture is proven below in sections 3 and 4.
3. Proof of the Orthocenter Conjecture
The orthocenter of each sub-triangle is a vertex of the main traingle.
- Given a point A, and three lines L1, L2 and L3, the following is assumed to be true: Given line L1 through point A and L2 perpendicular to L1 through point A, if L3 is again perpendicular to L2 through point A then L3 is the same line as L1.
- The orthocenter is the intersection of the altitudes of the triangle.
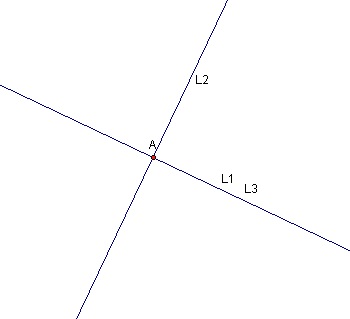
Figure 1: L1 equals L3
Let's look at the original construction again: figure 2 is the original triangle constucted with orthocenter and perpendicular altitudes drawn in light blue.
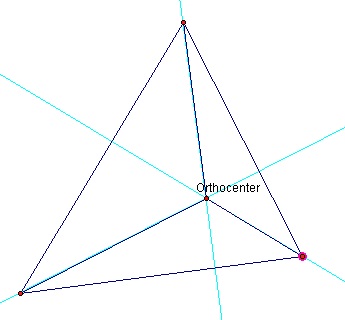
Figure 2: Main triangle with orthocenter
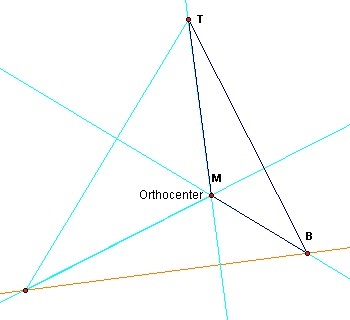
Here we have the sub-triangle highlighted (For the sake of simplicity let's refer to each of the three points of the sub-triangle as the bottom-, middle- and top point respectively):
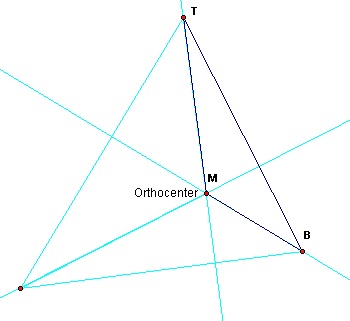
Figure 3: Sub-triangle highlighted
Constructing the orthocenter for the sub-triangle requires three perpendicular lines through each vertex. Let's start with point B:
The perpendicular line to TM passes through B, but TM lies on the perpendicular line through T which was used in drawing the main triangle's orthocenter. Therefore, this line is perpendicular to TM, through B by definition but so too is the base of the main triangle as it is perpendicular to TM by definition and through B because B is a vertex of the main triangle.
Furthermore:
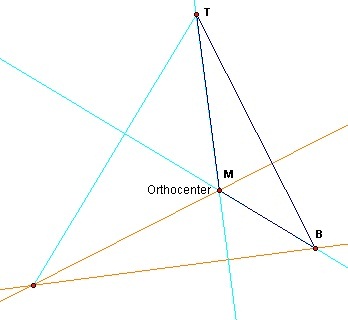
Figure 5: The altitude of M
Continuing this course of logic, we have:
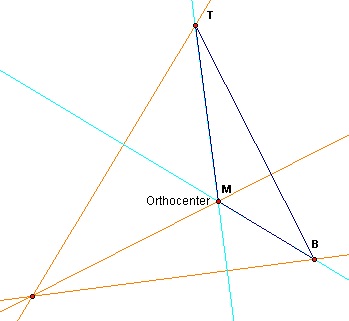
Figure 6: The altitude of T
The altitude of T is perpendicular to MB and passes through T by definition of an altitude. So too, this altitude lies on a side of the main triangle for the same reasoning used after figure 4.
Since these three altitudes are concurrent to the two sides and one altitude of the main triangle they must also meet at the same point as these three lines:
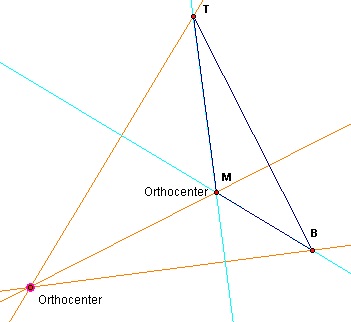
Figure 7: Orthocenter of triangle TMB
Therefore we have the orthocenter of TMB being the same point as a vertex of the main triangle. So too the orthocenters of the other two sub-triangles will also lie on points T and B respectively.
º
4. Proof of the Circumcircle Conjecture
The circumcircles are equal in size.
An advantage of using a tool like Geometer SketchPad is that we can play around with ideas and see whether our conjectures have any truth to them. Here's an example of one instance where the circumcircles have the same size:
Here we can see the respective centers and radii line up:
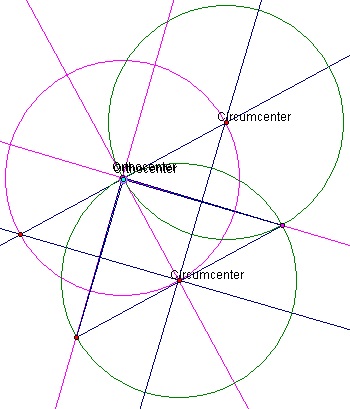
Figure 8: Possible equal-sized circles
One crictical part of this proof is that the main orthocenter is the shared point of all three sub-triangles and therefore must have the same distance from each circumcenter.
Given triangle ABC with orthocenter O, as in figure 9, we hide the three sides.
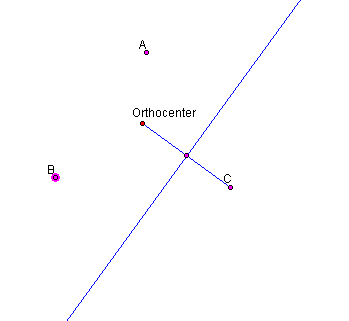
Figure 9
We repeat this process for OB and OA as in figure 10.
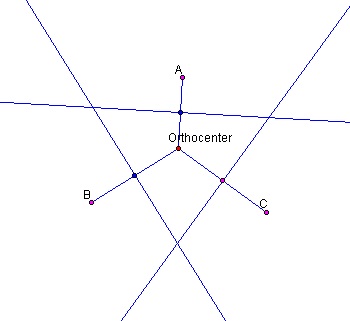
Figure 10
Lastly, we use the fast that the orthocenter (point O) is equidistant from each of the circumcenters by definition as it is part of the three points determining each of the three circumcircles. Therefore all three circumcircles have the same radius.
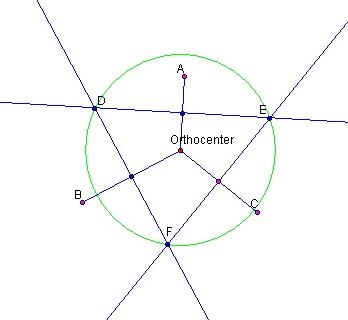
Figure 11
Here is a video to help visualize what the proof has entailed so far:
Finally, we need to show that the circumcircle of the equal to the other circumcircles.
Here is the circumcircle of the main triangle along with points D, E and F:
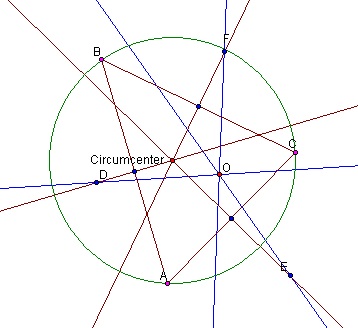
Figure 12
Here's a less complicated view of the same situation:
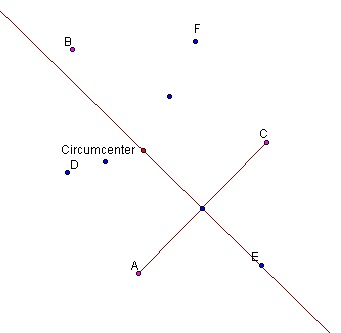
Figure 13
They both lie on the perpendicular bisector of AC because:
- The main circumcircle passes through A and C
- The circumcircle about point E passes through A and C
This implies that they are both equidistant from A and C.
It also seems that the circumcenter and the point E are both the same distance from the point of intersection between them. If this is proved then we have a parallelogram which would guarantee MC = EC which proves our conjecture.
This is the file with the construction of figure 12 given. Can you prove the conjecture MC = EC? Is there a better way to go about it?
In closing
Hopefully this investigation has shown some advantages of using tools in formulating conjectures and aiding in finding proof for these conjectures.