The parabola
Construction by using a line and a point
November 13, 2010
This investigation looks at an interesting way of constructing a parabola using a certain property that it has. The construction is done in Geometer SketchPad, you will need this application to view the original file if you want to.
Please note: you might need a plugin to play the animations in this page.
1. A definition
2. Construction of the parabola
3. Some applications of the parabola
1. A definition
A parabola can be defined by using any line and some fixed point (we are going to assume that the point is not on the line for simplicity). The parabola will contain all the points that are at the same distance from the point and the line.
For example:
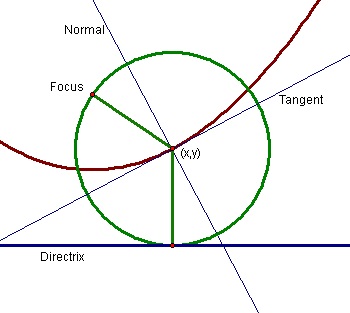
Figure 1
In figure 1 we havea parabola with a focus point and a thick blue line called the directrix. The parabola is the set of all points that are the same distance from the focus and the directrix, this is called the locus.
2. The construction
The construction is as follows:
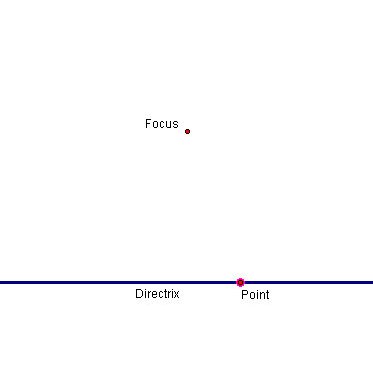
- Construct some line (L1) and a point (F for focus) that is not on the line.

- Construct a point (A) on the line
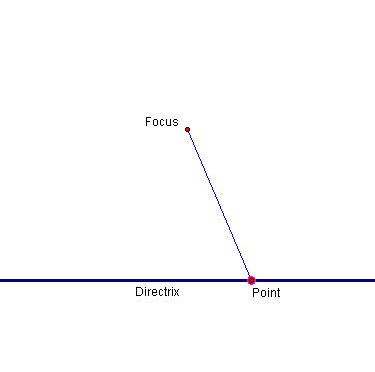
- Construct the line and midpoint of AF
- Construct the perpendicular bisector (P1) of AF
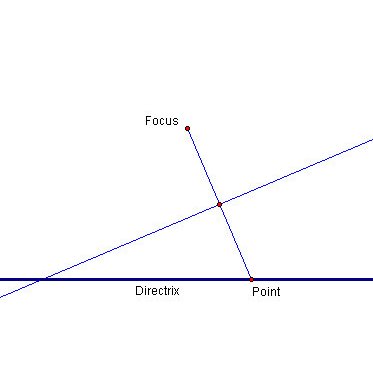
- Construct the perpendicular bisector (P2) to L1 though A
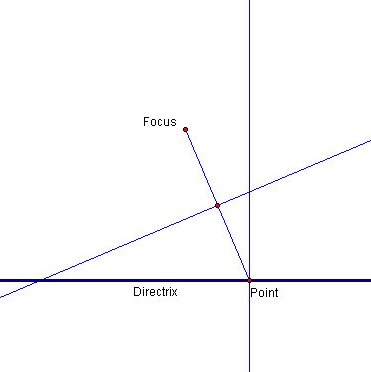
- Call the intersection of P1 and P2 point B
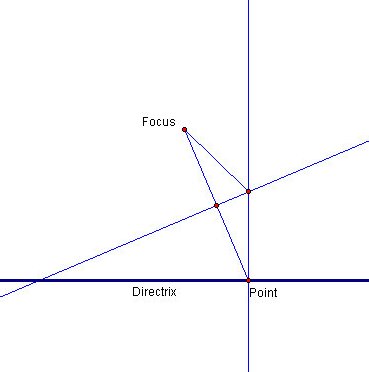
- Construct BF
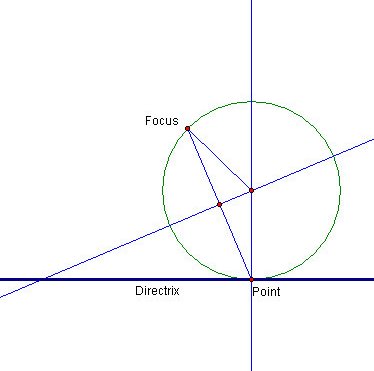
- Construct circle C center B, radius |BF|
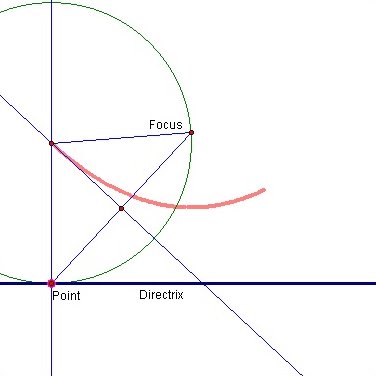
- Construct the locus of B as point A moves along the directrix (L1)
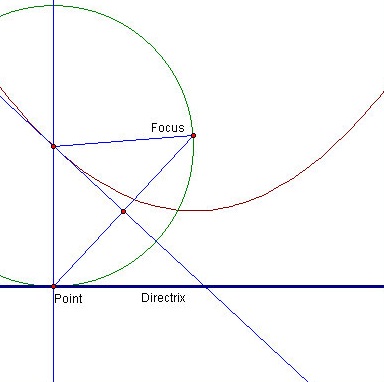
And here is the video showing the same construction:
We can also trace the movement of the tangent line:
3. Some applications of the parabola
- A general overwiew of the parabola can be found here.
And here are some pictures: