Triangles

Centroid, orthocenter and circumcenter.

 November 12, 2010

This investigation has a look at the three different centers of the triangle: the centroid, the orthocenter and the circumcenter. Each one will be constructed using Geometer SketchPad and then the trangle will be moved around to show the effect on each of these centers. Finally, all three centers will be constructed onto the same triangle and allowed to move around whilst tracing each individual point.

Please note: you might need a plugin to play the animations in this page.

is the point where all three medians of the triangle meet, with a median being the line from any vertex the middle of the opposite side.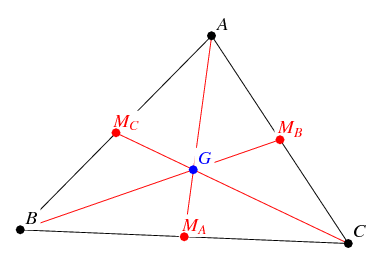

Given some triangle with vertices A,B and C we construct a midpoint for each side and then connect each vertex with its opposite midpoint.

This is one way of constructing a midpoint:


The centroid is then constructed using a midpoint tool, applied to a triangle and connecting the vertices with these midpoints:

2. The Orthocenter

The orthocenter is the intersection of the three lines that are dropped perpendicularly from each vertex onto the opposite side.
 

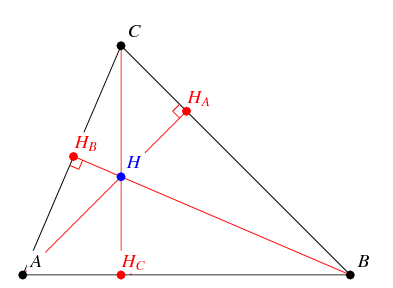
It is constructed as follows:

3. The Circumcenter

The circumcenter is the center of the circle that inscribes the triangle, in other words, the unique circle that goes through all three vertices of a given triangle.

A perpendicular bisector is a line that goes through the midpoint of a line AB and cuts it perpendicularly. This line gives us all possible points that are at equal distance from A and B simultaneously. By repeating this construction for lines BC and CA we get a point of intersection that is at equal distances from all three points A,B and C. Now we only have to construct a circle centered at this point of intersection, the radius to any point must also pass though the other two points as they are at equal distance from this point of intersection.

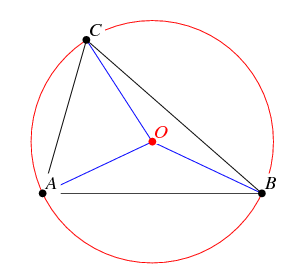
This is the construction:

4. Tracing all three points

Here we will use a triangle to show all three centers simulaneously. This trianlge will have a point fixed on some line that will be used to animate the triangle. Each of the three points will also leave tracing marks to highlight some interesting properties:



Interestingly, we get a parabola with a focal point where the centroid path meets the circumcenter path. The orthocenter's path is a parabola: the reason for this will be explored more in assignment 6.

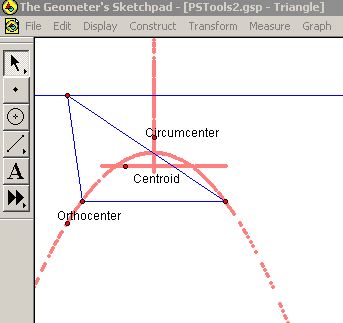
In closing

I hope this investigation has shown some interesting properties of triangle centers.