Pedal Triangles
November 23, 2010
This investigation looks at some properties of pedal triangles and makes use of Geometer SketchPad.
Please note: you might need a plugin to play the animations in this page.
2. The Conjecture and its Construction
3. Building Blocks of the Proof
4. Proof of the Pedal Triangle Conjecture
1. The Pedal Triangle
A pedal triangle is defined as the projection of some point onto a triangle.
Here is the definition on Wikipedia.
Here is the definition on Wolfram Mathworld.
This is what it looks like:
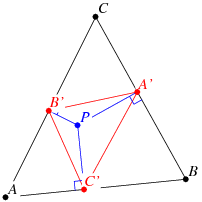
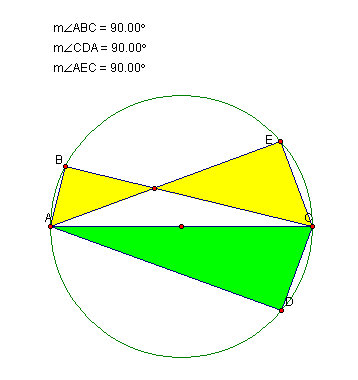
Figure 1: Pedal Tiangle of point P on triangle ABC
We find the pedal triangle by projecting point P onto each side of the triangle. Projection is done by constructing a perpendicular line onto some side, passing through P:
This process can be repeated for this pedal triangle again in the same way. Our problem look at repeating this process until we have a pedal triangle of a pedal triangle of a pedal triangle, known as the 3rd pedal triangle of ABC.
2. The Conjecture and its Construction
We want to show:
The proof is in showing that each respective angle of the two triangles are equal eg.The third pedal triangle is similar to the original triangle ABC
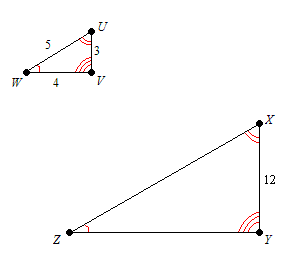
Figure 1: Two similar triangles
The construction is given in the video below, it makes use of a tool that draws a pedal triangle once its been given a point and the three vertices of the triangle. The tool can be downloaded here.
| So we need to show that triangle LJK is similar to ABC. |
3. Building Blocks of the Proof
Here are some important building blocks (B) we will be using for the proof:
4. Proof of the Conjecture
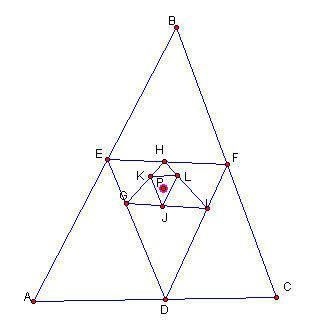
Figure 4.1: The problem
| To show that triangle LJK is similar to ABC. |
This is how we go about it:
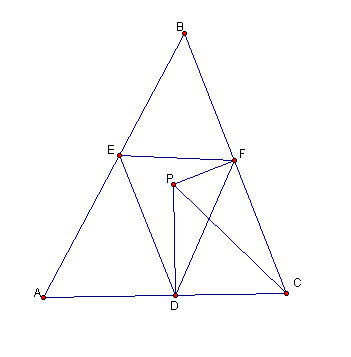
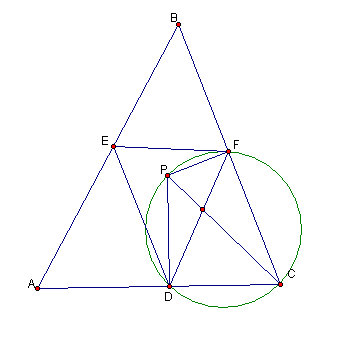
Figure 4.2: ABC and EFG
Here in Figure 4.2 we
simplify the problem by only showing the construction of the first two
triangles. Additionally, we construct PC, PF and PD. Recall that PF is
perpendicular to BC and PD to AC by construction (because that is the
definition of the projection of P onto BC and AC).
Figure 4.3 Using B1
We use the building block B1 in constructing this circle: PC is the diagonal of the circle though points P, F and C. D also lies on this line by sharing PC as a base with PFC and having right angle PDC.
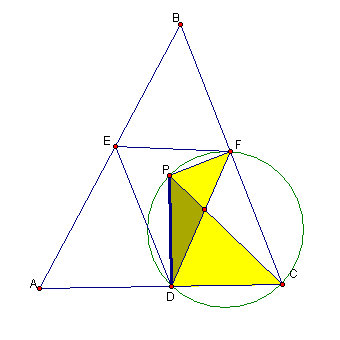
Figure 4.4: Using B2
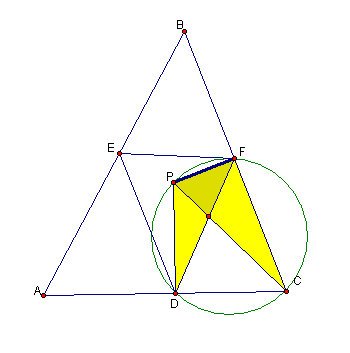
Figure 4.5: Using B2 again
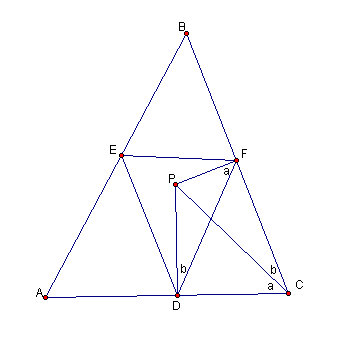
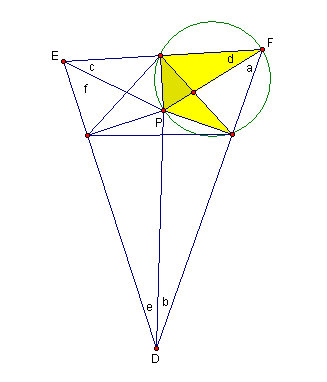
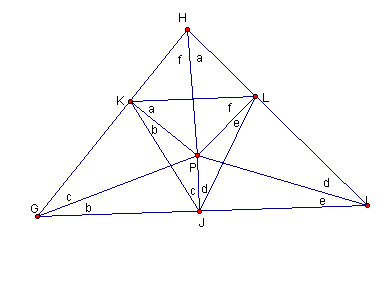
Figure 4.6: Naming the angles
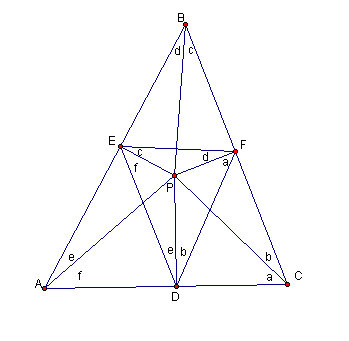
Figure 4.7: Naming all angles
In the same way as figure 4.6, we split angle ABC and angle CAB into two parts and apply the same reasoning to get angles a though f into the first pedal triangle.
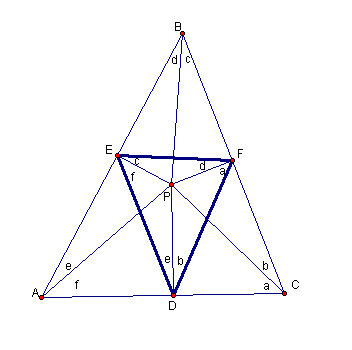
Figure 4.8 The first pedal triangle
Let's have a closer look at figure the first pedal triangle.
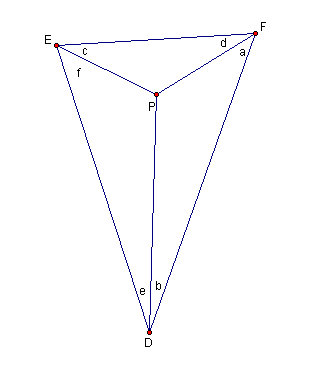
Figure 4.9: Only the first pedal triangle.
We will go to work on this triangle using the same reasoning as with the main triangle.
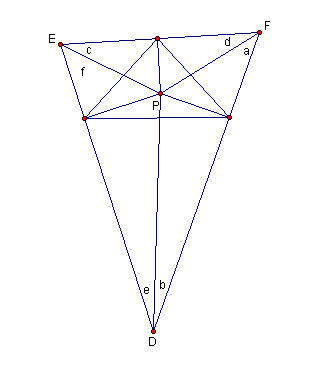
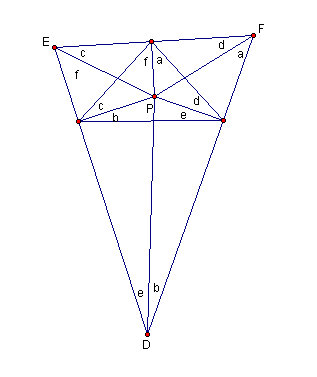
Figure 4.10: The second pedal triangle
This is the second pedal triangle constructed inside the first.
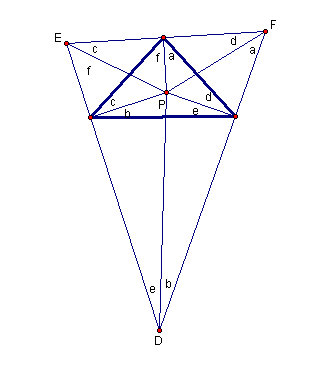
Figure 4.13: The second pedal triangle
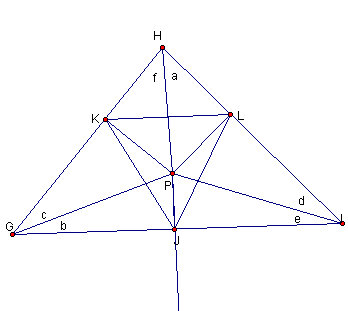
4.14: The third pedal triangle inside the first
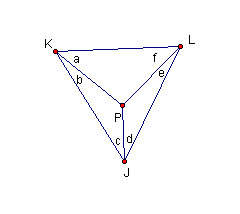
Figure 4.17: The third pedal triangle
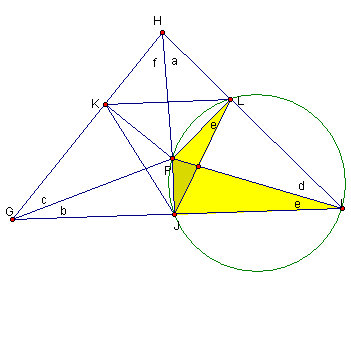
Finally, by comparing with Figure 4.7, we have
- angle JKL = a + b = angle ACB
- angle KJL = c + d = angle CBA
- angle JLK = e + f = angle BAC
Therefore:

| Triangle JKL is similar to triangle CBA. |
In closing
Remember that when we work with proofs and conjectures, we try to find all applicable building blocks that can be applied to the problem and then, systematically, sift out as much information as possible using the given facts and also the comparisons that can be made using what we know.
There are usually many ways to solve a given problem and reaching dead-ends are sometimes vital in reaching a solution.