Circles and areas
November 24, 2010
This investigation looks at some properties of circles and areas and makes use of Geometer SketchPad. You can download the file here and manipulate it using Geometer SketchPad if you have a copy.
Please note: you might need a plugin to play the animations in this page.
1. The Problem
2. Symmetry
3. A solution
1. The problem
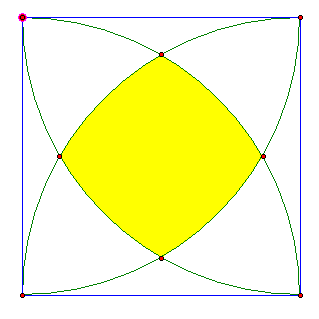
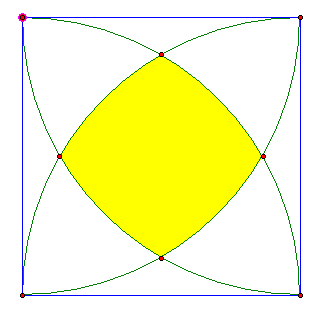
Given:
- A square of side s
- Four quarter circles of radius s constructed as above
- The area of the yellow region.
2. Symmetry
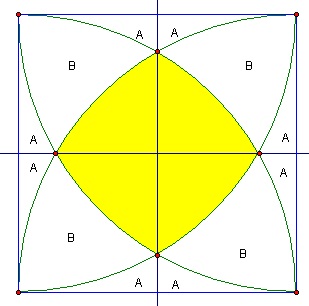
The motivation for the symmetry is that the radii are the same from each of the vertixes, therefore the intersection of two arcs on the same line will halve that line and the areas enclosed will be equal (as shown above).
3. A solution
Look at only one of the arcs and disregard the others.
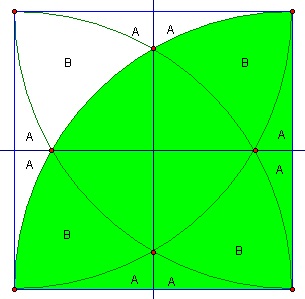
We can find the larger area by taking a quarter of the area of a circle with radius s.
Then we have:
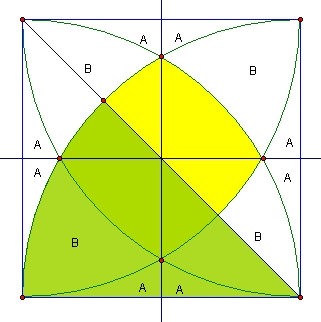
total area - green area = A + A +
B + A + A
But the yellow area =
= total area - (A+A+B+A+A+B+A+A+B+A+A+B)
= total area - 8A + 4B
So if we can find A and B, we have a solution:
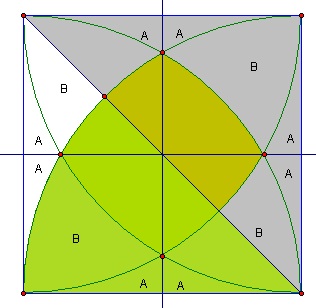
Construct a duplicate of the square directly adjacent to the original, along with a triangle:
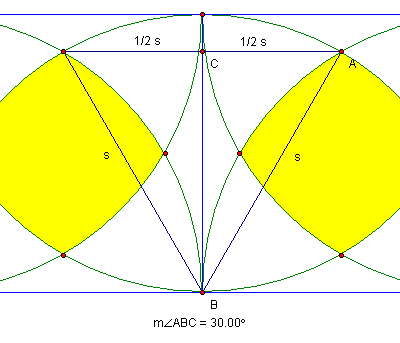
As the vertices of the triangle lie on the intersections of equal radii, at starting points of a distance of s from each other, we have a length of a half of s for each side. We also have angle of 30 degrees (pi/12) for angle ABC as it is an equilateral triangle (three 60 degree angles) split into two halves of 30 degrees each.
Now we construct the interior of the sector:
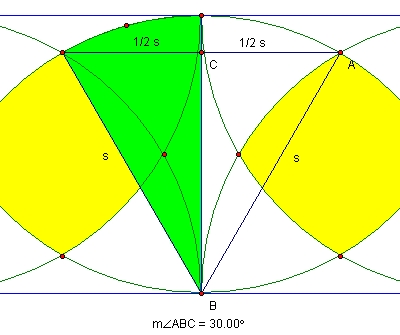
We have the radius and angle of the sector so we can find the area using the formula(note that we'll be working in radians from here on) Area = (theta/2)*r^2
We can also construct this triangle to help us find the area of A:
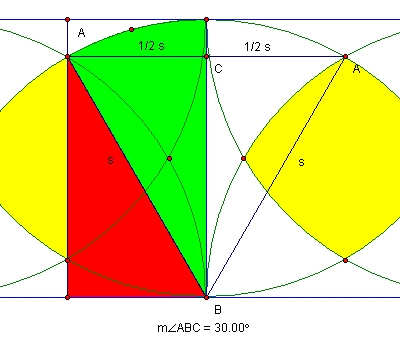
The area of A + green + red is half of the square i.e. s^2. We can now do the following calculations:
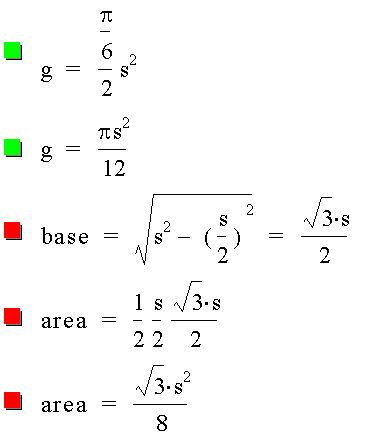
We find A by sustracting the green and red areas from half of the square's area:
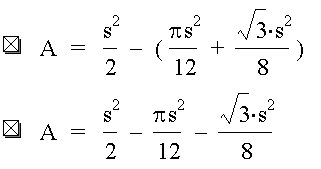
Let's rather work with real numbers:
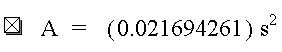
Consider the following, we are again working with half of the square, only diagonally this time:
We have a green sector which is exactly half of a quarter sector, which is therefore an angle of 2pi/8 or more simply pi/4.
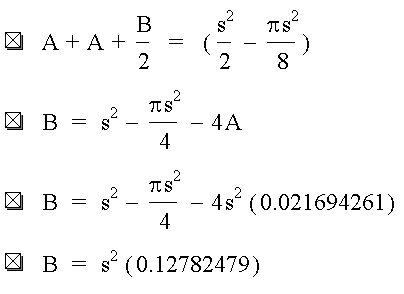
Putting it all together: we take the area of the entire square and subtract 4B's and 8A's

In other words, that inscribed yellow area takes up about 32% of the square.
This is not an elegant solution though because the values have been rounded and calculated, had we stuck to our fractions and pi's, this is what we would have ended up with:
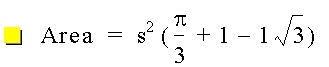
The advantage of this form above being nicer to look at it, is that it's infinitely more accurate than the decimal form; to be more precise:
it is accurate.